Matemática no Enem
A prova de matemática do Enem (Matemática e suas tecnologias) é a única prova que apresenta uma disciplina isolada, o que a torna o maior peso individual do concurso.
As questões da prova são objetivas, com 5 alternativas de resposta, apresentam enunciados contextualizados e cobram um conhecimento global do aluno.
Conteúdos que mais caem na prova de matemática
Veja os conteúdos de Matemática mais cobrados no Enem dos últimos 9 anos:
1. Grandezas proporcionais
Grandezas proporcionais, que engloba os conteúdos de razão e proporção, regra de três, porcentagem e escalas, é o que mais aparece nas questões de Matemática.
O fato deste conteúdo ser aplicado nas mais variadas situações do cotidiano, faz com que seja muito explorado no Enem.
Esse tipo de cálculo pode aparecer em questões que cobrem diretamente a relação entre grandezas ou em problemas onde este cálculo é usado em uma das etapas da sua resolução.
Exemplo
(Enem - 2017) Às 17 h 15 min começa uma forte chuva, que cai com intensidade constante. Uma piscina em forma de um paralelepípedo retângulo, que se encontrava inicialmente vazia, começa a acumular a água da chuva e, às 18 horas, o nível da água em seu interior alcança 20 cm de altura. Nesse instante, é aberto o registro que libera o escoamento da água por um ralo localizado no fundo dessa piscina, cuja vazão é constante. Às 18 h 40 min a chuva cessa e, nesse exato instante, o nível da água na piscina baixou para 15 cm.
O instante em que a água dessa piscina terminar de escoar completamente está compreendido entre
a) 19 h 30 min e 20 h 10 min
b) 19 h 20 min e 19 h 30 min
c) 19 h 10 min e 19 h 20 min
d) 19 h e 19 h 10 min
e) 18 h 40 min e 19 h
Leia sobre proporção.
2. Estatística, gráficos e tabelas
Cálculo de média, moda e mediana são os conteúdos de estatística que mais aparecem na prova de Matemática. Além disso, as questões que envolvam a interpretação de gráficos (estatísticos ou não) e tabelas são muito recorrentes.
Aliás, os gráficos estão presentes não só na prova de Matemática, mas também de outras disciplinas como Física, Geografia, Biologia e Química.
Na prova de Matemática, muitas vezes, a interpretação do gráfico é apenas uma etapa da resolução da questão, sendo necessário aplicar outros conhecimentos.
Exemplo
(Enem - 2017) Dois reservatórios A e B são alimentados por bombas distintas por um período de 20 h. A quantidade de água contida em cada reservatório nesse período pode ser visualizada na figura.
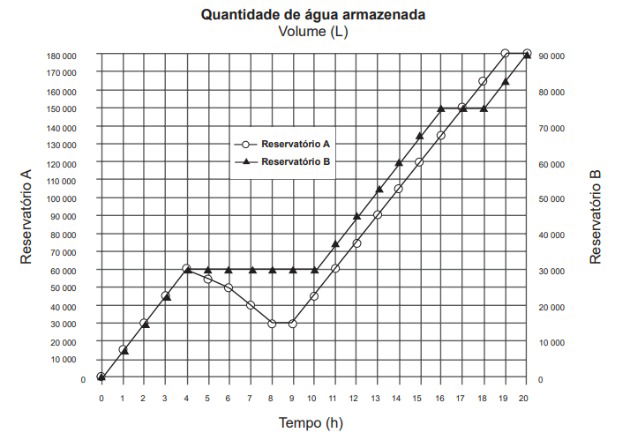
O número de horas em que os dois reservatórios contêm a mesma quantidade de água é
a) 1.
b) 2.
c) 4.
d) 5.
e) 6.
3. Aritmética
Questões com cálculos simples, que envolvam frações ou números decimais, problemas relacionados com princípio da contagem, também aparecem com frequência.
Exemplo
(Enem - 2017) Em um parque há dois mirantes de alturas distintas que são acessados por elevador panorâmico. O topo do mirante 1 é acessado pelo elevador 1, enquanto que o topo do mirante 2 é acessado pelo elevador 2. Eles encontram-se a uma distância possível de ser percorrida a pé, e entre os mirantes há um teleférico que os liga que pode ou não ser utilizado pelo visitante.
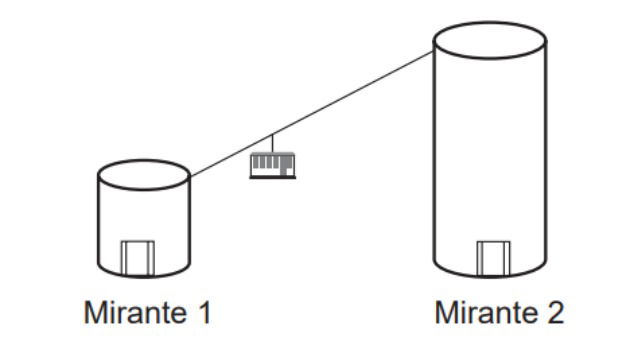
O acesso aos elevadores tem os seguintes custos:
- Subir pelo elevador 1: R$ 0,15;
- Subir pelo elevador 2: R$ 1,80;
- Descer pelo elevador 1: R$ 0,10;
- Descer pelo elevador 2: R$ 2,30.
O custo da passagem do teleférico partindo do topo do mirante 1 para o topo do mirante 2 é de R$ 2,00, e do topo do mirante 2 para o topo do mirante 1 é de R$ 2,50.
Qual é o menor custo, em real, para uma pessoa visitar os topos dos dois mirantes e retornar ao solo?
a) 2,25
b) 3,90
c) 4,35
d) 4,40
e) 4,45
4. Geometria plana e espacial
Saber calcular a área das principais figuras planas e o volume dos sólidos geométricos é bastante importante, pois esse conteúdo aparece com frequência na prova.
Além disso, podem aparecer questões que envolvam uma visão espacial, planificações, teorema de Pitágoras e cálculo de perímetro.
Exemplo
(Enem - 2017) Um garçom precisa escolher uma bandeja de base retangular para servir quatro taças de espumante que precisam ser dispostas em uma única fileira, paralela ao lado maior da bandeja, e com suas bases totalmente apoiadas na bandeja. A base e a borda superior das taças são círculos de raio 4 cm e 5 cm, respectivamente.

A bandeja a ser escolhida deverá ter uma área mínima, em centímetro quadrado, igual a
a) 192.
b) 300.
c) 304.
d) 320.
e) 400.
5. Funções
Na prova é cobrado com frequência função afim, função quadrática, função Exponencial e função logarítmica, além da lei de formação de uma função e o seu gráfico.
Exemplo
(Enem - 2017) Para realizar a viagem dos sonhos, uma pessoa precisava fazer um empréstimo no valor de R$ 5 000,00. Para pagar as prestações, dispõe de, no máximo, R$ 400,00 mensais. Para esse valor de empréstimo, o valor da prestação (P) é calculado em função do número de prestações (n) segundo a fórmula
Se necessário, utilize 0,005 como aproximação para log 1,013; 2,602 como aproximação para log 400; 2,525 como aproximação para log 335.
De acordo com a fórmula dada, o menor número de parcelas cujos valores não comprometem o limite definido pela pessoa é pela pessoa é
a) 12.
b) 14.
c) 15.
d) 16.
e) 17.
Para mais exercícios de função, veja também:
- Exercícios de Função Afim
- Função Quadrática - Exercícios
- Função Exponencial - Exercícios
- Logaritmo - Exercícios
6. Probabilidade
Para esse conteúdo não basta apena saber as fórmulas de probabilidade, é fundamental saber aplicá-las dentro do contexto proposto no enunciado.
Exemplo
(Enem - 2017) Um morador da região metropolitana tem 50% de probabilidade de atrasar-se para o trabalho quando chove na região; caso não chova, sua probabilidade de atraso é de 25%. Para um determinado dia, o serviço de meteorologia estima de 30% a probabilidade da ocorrência de chuva nessa região.
Qual é a probabilidade de esse morador se atrasar para o serviço no dia para o qual foi dada a estimativa de chuva?
a) 0,075
b) 0,150
c) 0,325
d) 0,600
e) 0,800
Quiz de Matemática Enem
Dicas para ir bem na prova de Matemática
A prova de Matemática é composta por questões de diferentes níveis de dificuldade e é obvio que quanto mais questões o aluno resolver sem "chutar" melhor.
Desta forma, o ideal é fazer as questões mais fáceis primeiro. Assim, o estudante assegurará que não deixará de acertar essas questões por não ter tido tempo de fazê-las.
As questões, por serem contextualizadas, normalmente são muito extensas. Então, uma dica é sublinhar as informações mais importantes, desta forma evita-se ler várias vezes a mesma questão.
Os gráficos, tabelas e infográficos aparecem com muita frequência na prova. Muitas vezes, a correta interpretação desses recursos é suficiente para acertar a questão.
Assim, antes de tirar conclusões precipitadas, observe as grandezas envolvidas olhando os eixos, identifique as escalas e unidades usadas e veja o seu título. Tudo isso pode fazer uma grande diferença nesse tipo de questão.
Como a prova possui muitas questões e pouco tempo para a sua resolução, o aluno deverá, sempre que possível, simplificar os cálculos.
Para ganhar minutos preciosos poderá, por exemplo, aplicar produtos notáveis em potenciações, fazer aproximações, estimativas e cálculo mental, substituir números muito grandes por potências de 10 e simplificar frações.
Leia também sobre:
Como se preparar para ir bem na prova de Matemática
Para começar, faça as pazes com essa matéria. Muitos alunos criam uma relação muito ruim com a Matemática e acabam acreditando que nunca conseguirão ter um bom desempenho nesta disciplina.
Ter essa crença só dificultará o seu aprendizado e portanto, deixe-se envolver com os encantos dos números! Acredite, você pode realmente aprender Matemática e corre ainda o risco de acabar gostando.
Para isso, comece a se preparar fazendo uma revisão dos conteúdos do ensino fundamental. Esses conteúdos, além de serem a base para o aprendizado, são também cobrados no Enem.

Crie o hábito de resolver os exercícios sem usar a calculadora. Não é permitido o seu uso na prova e sem saber fazer as operações fundamentais será muito difícil tem um bom desempenho.
Além disso, procure aprender técnicas que facilitam as contas, pois o tempo tem um peso muito grande nesta prova.
Uma boa sugestão é anotar quantos minutos leva para fazer cada questão e ir tentando sempre fazer em um menor tempo.
O ponto de partida para resolver uma questão de Matemática é a interpretação. Principalmente no Enem, onde as questões são contextualizadas, entender o enunciado é fundamental.
Desta forma, ler todos os dias textos dos mais variados temas, não só de Matemática, podem ajudar a melhorar a leitura e interpretação.
E por último, mas não menos importante, faça exercícios. Procure se familiarizar com o formato das questões do Enem, resolvendo provas de anos anteriores.
Procure resolver as questões sozinho primeiro. Se não conseguir resolver, não olhe imediatamente o gabarito. Tente novamente depois de um tempo, ser perseverante é fundamental.
Conforme for acertando as questões que fizer sozinho, ganhará mais confiança e passará a gostar mais de aprender Matemática, garanto.
Leia também:
Assuntos que mais caem no Enem
Questões de Matemática no Enem
GOUVEIA, Rosimar. Matemática no Enem. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/matematica-no-enem/. Acesso em:


