Questões para Olimpíada de Matemática Nível 3 (Ensino Médio)
Se prepare (ou ajude os seus alunos a se preparem) para a OBMEP, a Olimpíada Brasileira de Matemática das Escolas Públicas e Particulares.
Esta lista possui questões originais, inspiradas nas questões da OBMEP, para o Nível 3 (Ensino Médio). Todas as questões possuem soluções explicadas.
Questão 1
Três amigos — Alice, Bob e Carlos — dividem um táxi para percorrer 30 km. Cada um tem um destino em diferentes pontos do percurso:
- Alice desce no primeiro ponto, aos 10 km.
- Bob desce no segundo ponto, aos 20 km.
- Carlos desce no terceiro e último ponto, aos 30 km.
A corrida custou R$ 48,00. Eles estão discutindo uma maneira justa de dividir esse valor.
Se eles decidirem dividir o valor proporcionalmente à distância percorrida por cada um, quanto cada amigo deve pagar?
A) Alice: R$ 5,00, Bob: R$ 12,50, Carlos: R$ 27,50
B) Alice: R$ 8,00 Bob: R$ 16,00, Carlos: R$ 24,00
C) Alice: R$ 10,00, Bob: R$ 15,00, Carlos: R$ 20,00
D) Alice: R$ 15,00, Bob: R$ 15,00, Carlos: R$ 15,00
E) Alice: R$ 9,00, Bob: R$ 13,50, Carlos: R$ 22,50
Para resolver, divida o custo proporcionalmente aos quilômetros que cada um percorreu:
- Alice percorreu 10 km (1/3 da distância).
- Bob percorreu 20 km (também 2/3 da distância).
- Carlos percorreu 30 km (3/3 da distância).
Assim, Bob deve pagar o dobro de Alice e, Carlos, o triplo de Alice.
- 1 parte para Alice;
- 2 partes para Bob;
- 3 partes para Carlos.
Um total de seis partes. Assim, vamos dividir o total por 6:
48 / 6 = 8
Cada parte é igual a R$ 8,00. Logo:
- Alice: 1 parte = R$ 8,00.
- Bob: 2 partes = R$ 16,00.
- Carlos: 3 partes = R$ 24,00.
Conferindo o total:
8 + 16 + 24 = 48
Questão 2
Considere um círculo. Marque dois pontos quaisquer na circunferência que o determina e chame-os de P e Q. Agora, escolha um terceiro ponto aleatoriamente na circunferência e chame-o de X.
Qual é, aproximadamente, a maior probabilidade do triângulo formado pelos pontos P, Q e X "envolver" o centro do círculo? Ou seja, qual a probabilidade de que o centro do círculo fique dentro triângulo?
a) 25%
b) 33,33%
c) 50%
d) 66,67%
e) 75%
1. Visualização:
Círculo: desenhe um círculo em um papel e marque os pontos P e Q em qualquer lugar da circunferência.
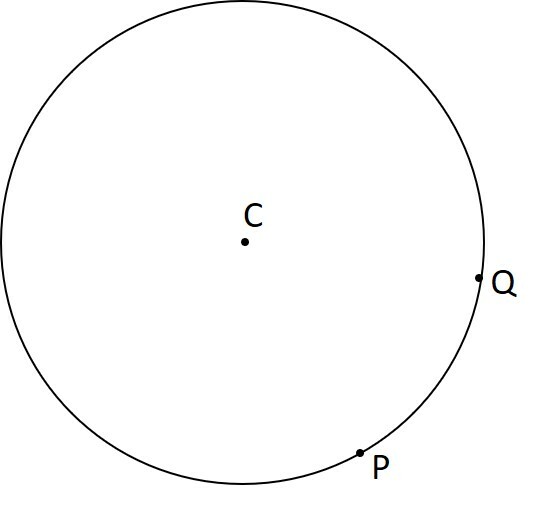
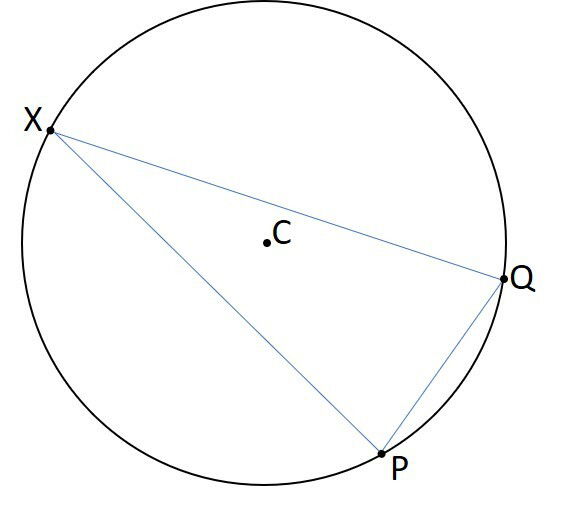
Triângulo: marque um ponto X e conecte os pontos P, Q e X com linhas retas. Você formará um triângulo.
Condição: para que o triângulo "envolva" o centro C, o ponto X precisa estar em determinados pontos da circunferência.
Por exemplo:
Alinhando Q, C e X, chamando X de Qʼ, no outro extremo, alinhando P, C e X, chamando X de Pʼ, temos:
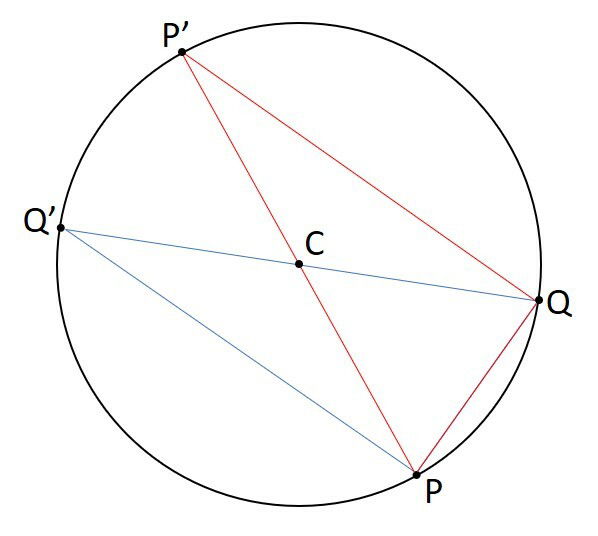
Veja que X pode ser qualquer ponto do arco , ou seja:
.
2. Analisando a probabilidade:
A probabilidade é calculada como a razão entre os casos favoráveis pelos casos totais.
Os casos favoráveis são todos os pontos X que pertencem ao arco PʼQʼ.
Os casos totais são os pontos da circunferência. O comprimento da circunferência é dado por:
Onde r é o raio da circunferência.
Substituindo na fórmula da probabilidade:
Logo, a probabilidade é máxima quando o arco PʼQʼ é máximo.
3. Arco PʼQʼ máximo:
O comprimento do arco PʼQʼ é igual ao comprimento do arco PQ. Veja que o ângulo central é o ângulo que determina os arcos. Pela propriedade dos ângulos opostos pelo vértice, temos que PCQ = PʼCQʼ.
Portanto, qual é a situação em que os pontos P e Q estão mais afastados? A resposta é que estão mais afastados quando estão a meia circunferência um do outro.
No exato ponto que o arco PʼQʼ = 180º, ou seja, , os três pontos Pʼ, C e Qʼ são colineares e, portanto, não formam um triângulo.
Vamos considerar o ponto exatamente anterior a 180º.
4. Cálculo da probabilidade:
Substituindo o valor do arco máximo na fórmula da probabilidade:
Resposta correta: c) 50%
Questão 3
Qual das alternativas abaixo apresenta a justificativa correta para que, dentre todos os retângulos de perímetro fixo, o quadrado possui a maior área?
a) A área do quadrado é sempre um número perfeito.
b) O quadrado possui os quatro lados iguais, o que maximiza a área.
c) A diagonal do quadrado é a maior possível para um dado perímetro.
d) A área do retângulo pode ser expressa como uma função quadrática com concavidade para baixo, cujo valor máximo ocorre quando o retângulo é um quadrado.
e) A área do quadrado é diretamente proporcional ao quadrado de seu lado, enquanto a área do retângulo é diretamente proporcional ao produto de seus lados.
A alternativa d) é a correta.
Ela expressa de forma clara e concisa a ideia de que a área do retângulo pode ser representada por uma função quadrática que o ponto máximo dessa função corresponde ao caso em que o retângulo é um quadrado.
Demonstração:
Seja "P" o perímetro fixo do retângulo:
P = 2x + 2y, onde x e y são as medidas dos lados do retângulo.
A área do retângulo é dada por:
A = x * y
Isolando y na equação do perímetro:
y = (P - 2x) / 2
Substituindo y na equação da área:
A = x * (P - 2x) / 2
A = (Px - 2x²) / 2
ou
Analisando a função quadrática:
A função representa uma parábola com concavidade para baixo.
O ponto máximo dessa parábola representa a maior área possível.
O vértice da parábola corresponde ao valor de x que maximiza a função.
Calculando o vértice da parábola:
O vértice de uma parábola da forma y = ax² + bx + c ocorre em x = -b/2a.
No nosso caso, a = -1, b = P/2.
Logo,
Substituindo x por P/4 na equação do perímetro, encontramos y = P/4.
Conclusão:
O valor de x que maximiza a área é P/4.
O valor de y também é P/4.
Portanto, para obter a maior área, x e y devem ser iguais, ou seja, o retângulo é um quadrado.
OUTRA PROVA MATEMÁTICA
Seja P o perímetro do retângulo e b e h sua base e altura respectivamente. Logo, sua área A é definida por:
A = b . h
O perímetro é definido como:
P = 2b + 2h.
Área do quadrado em função do perímetro (P):
Como o quadrado possui quatro lados iguais, em relação ao perímetro P, cada um de seus lados (L) é:
Assim, a área do quadrado em função do perímetro é:
Como o retângulo é um quadrado deformado em d unidades para mais e para menos em relação a sua base e altura:
Neste ponto, podemos utilizar o produto notável: produto da soma pela diferença resultando em uma diferença de dois quadrados.
Comparação entre a área do quadrado e do retângulo:
Conclusão:
Com a desigualdade acima, vemos claramente que a área do retângulo é sempre menor que a área do quadrado, assumindo que ambos possuem o mesmo perímetro.
Outras alternativas:
a): Não há relação entre a área ser um número perfeito e ser máxima.
b): Embora a igualdade dos lados seja uma característica do quadrado, essa afirmação por si só não justifica a maximização da área.
c): A diagonal não é diretamente relacionada à área máxima.
e): Essa afirmação é verdadeira, mas não explica por que o quadrado maximiza a área.
Questão 4
Cinco amigos – Carlos, Bruno, Felipe, Guilherme e Igor – foram à casa do João para uma tarde de jogos. Carlos chegou depois de Bruno, mas antes de Guilherme. Já Felipe, Guilherme e Igor chegaram um após o outro, nessa ordem.
Quem foi o primeiro a chegar?
A) Carlos
B) Bruno
C) Felipe
D) Guilherme
E) Igor
Analisando a primeira pista:
"Carlos chegou depois de Bruno, mas antes de Guilherme."
Isso indica que a ordem entre esses três amigos é:
Bruno chegou antes de Carlos, e Carlos chegou antes de Guilherme.
A ordem parcial que temos até agora é: Bruno → Carlos → Guilherme
Analisando a segunda pista:
"Felipe, Guilherme e Igor chegaram um após o outro, nessa ordem."
Isso significa que:
Felipe chegou imediatamente antes de Guilherme e Guilherme chegou imediatamente antes de Igor.
A sequência completa desses três amigos é, então: Felipe → Guilherme → Igor
Uma opção seria:
Bruno → Felipe → Carlos → Guilherme → Igor
Esta opção satisfaz a pista 1(Bruno → Carlos → Guilherme), mas viola a pista 2, que afirma que Felipe → Guilherme → Igor chegaram nesta ordem.
Assim, a única opção possível é:
Bruno → Carlos → Felipe → Guilherme → Igor
Conclusão:
Bruno foi o primeiro a chegar.
Questão 5
Uma folha de papel no formato retangular de lados: L (largura) e H (altura), foi dobrada como na figura:
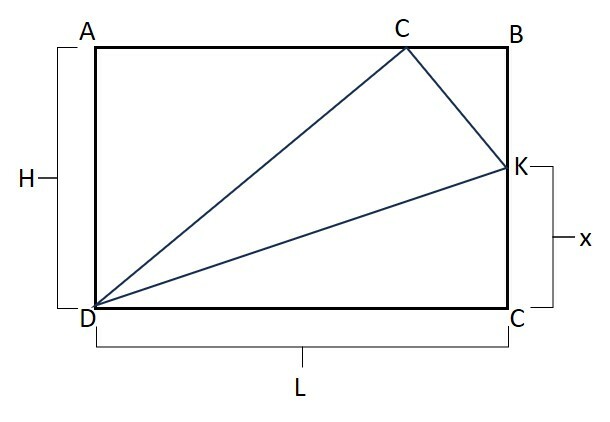
O retângulo ABCD da folha teve o vértice C sobreposto ao lado AB. O ponto K representa o ponto onde ocorreu a dobra.
Qual expressão representa o percentual das áreas dos triângulos ACD e CBK juntas, em relação à área original da folha de papel?
a)
b) L²x . 100
c)
d)
e)
Sendo um retângulo, a área original da folha é:
Onde, L é a largura e H é a altura.
Os triângulos DCK (a parte sobreposta) e DKC (parte "vazia") são iguais. Eles representam a porção da folha que foi dobrada, portanto, iguais.
Logo, a área dos triângulos ACD + CBK é iguai a área total original (LH) menos duas vezes DCK.
A fórmula da área de um triângulo é:
No triângulo DKC a base é o próprio lado L, enquanto a altura é x. Logo:
Para o cálculo do percentual:
Devemos nos perguntar: qual número p (percentual) devemos multiplicar a área original para resultar em ACD + CBK?
Questão 6
Ana pensou em um número e realizou as seguintes operações:
- Multiplicou o número por 3.
- Somou 8 ao resultado.
- Dividiu o total por 2.
- Subtraiu 6.
- Tirou a raiz quadrada do número final e obteve 5.
O resultado após a raiz quadrada foi 5.
Qual é a soma dos algarismos do número em que Ana pensou?
a) 8
b) 9
c) 10
d) 11
e) 12
Chamaremos este número pensado por Ana de x. Após todas as operações, o resultado foi 5.
A estratégia que utilizaremos para determinar o número pensado por Ana é realizar as operações inversas, de "traz para frente".
A quinta operação foi a radiciação, por isso, utilizaremos a potenciação. Como o resultado foi 5, faremos 5².
5² = 25
A quarta operação foi a subtração, por isso, faremos adição. Coma ela havia subtraído 6, agora, somamos 6.
25 + 6 = 31
A terceira operação foi a divisão, desta forma, faremos a multiplicação. Como ela dividiu por 2, multiplicaremos por 2.
31 x 2 = 62
A segunda operação foi a soma, de modo que faremos uma subtração.
62 - 8 = 54
A primeira operação foi a multiplicação, por isso, faremos divisão. Como Ana havia multiplicado por 3, faremos a divisão por 3.
54 / 3 = 18
Conclusão:
O número pensado por Ana foi 18, logo, a soma dos algarismos é 9.
1 + 8 = 9
Questão 7
Para mais questões para OBMEP (Olimpíada de Matemática):
- Questões para Olimpíada Mirim 1 OBMEP.
- Questões para Olimpíada Mirim 2 OBMEP
- Questões para Olimpíada de Matemática (8º e 9º ano do Fundamental II)
- Questões para Olimpíada de Matemática (6º e 7º ano do Fundamental II)
Veja também:
- 27 charadas de matemática com resposta
- 27 exercícios de Matemática Básica
- Exercícios de Raciocínio Lógico: 19 questões com respostas
- Teste de raciocínio lógico (com respostas e pontuação)
- Lógica Matemática
- Desafios matemáticos para estimular seu raciocínio
Referências Bibliográficas
OBMEP. Olimpíada Brasileira de Matemática das Escolas Públicas. Disponível em: http://www.obmep.org.br/. Acesso em: 24 out. 2024.
ASTH, Rafael. Questões para Olimpíada de Matemática Nível 3 (Ensino Médio). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/questoes-para-olimpiada-de-matematica-obmep-nivel-3/. Acesso em:


