Questões para Olimpíada de Matemática (8º e 9º ano do Fundamental II)
Pratique para a OBMEP, a Olimpíada Brasileira de Matemática das Escolas Públicas e Particulares.
Esta lista possui questões originais, inspiradas nas questões da OBMEP, para o Nível 2 (8º e 9º anos). Todas as questões possuem soluções explicadas.
Questão 1
Em uma fábrica de cadeiras, cada máquina consegue produzir uma cadeira em 2 minutos. No entanto, uma máquina quebra após funcionar por 512 minutos. Sabendo que essa máquina dobra sua capacidade de produção a cada 64 minutos de funcionamento, quantas cadeiras ela terá produzido antes de quebrar?
A) 2560
B) 640
C) 8160
D) 1280
E) 5120
Entendimento do problema:
- Uma máquina produz uma cadeira a cada dois minutos.
- Ela quebra após 512 minutos.
- A cada 64 minutos, a máquina dobra a capacidade de produção.
Dividir o tempo total em intervalos de 64 minutos:
512 dividido por 64 é igual a oito intervalos.
Isso significa que a capacidade da máquina dobra oito vezes ao longo de seu funcionamento.
Calcular a capacidade de produção em cada intervalo de sessenta e quatro minutos:
Listamos a capacidade de produção de cada intervalo, considerando que ela dobra a cada 64 minutos:
- No primeiro intervalo de 64 minutos: uma cadeira a cada dois minutos.
- No segundo intervalo: duas cadeiras a cada dois minutos.
- No terceiro intervalo: quatro cadeiras a cada dois minutos.
E assim por diante, duplicando a cada intervalo.
Calcular o número de cadeiras produzidas em cada intervalo de 64 minutos:
Cada intervalo de 64 minutos contém 32 períodos de dois minutos.
Portanto, o número de cadeiras produzidas em cada intervalo é:
Primeiro intervalo: 32 cadeiras
Segundo intervalo: 64 cadeiras
Terceiro intervalo: 128 cadeiras
Quarto intervalo: 256 cadeiras
Quinto intervalo: 512 cadeiras
Sexto intervalo: 1024 cadeiras
Sétimo intervalo: 2048 cadeiras
Oitavo intervalo: 4096 cadeiras
Somar o total de cadeiras produzidas:
Total de cadeiras = 32 + 64 + 128 + 256 + 512 + 1024 + 2048 + 4096, o que dá 8160 cadeiras.
A máquina terá produzido 8160 cadeiras antes de quebrar.
Questão 2
Isadora está preparando uma receita de bolo.
- Primeiro, ela coloca 500 ml de leite no liquidificador;
- Em seguida, precisa adicionar água, na quantidade de 35% da quantidade de leite;
- Depois, ela deve acrescentar óleo na quantidade de 10% do líquido total que já está no liquidificador.
Por último, Isadora completará a mistura no liquidificador com suco de laranja até que o total de líquido seja 1 litro. Quantos mililitros de suco de laranja ela deve adicionar?
a) 87,5 ml
b) 157 ml
c) 257,5 ml
d) 735 ml
e) 853,5 ml
Passo 1: cálculo da quantidade de água.
35% de 500 ml
Passo 2: leite mais água.
500 + 175 = 675 ml
Passo 3: cálculo da quantidade de óleo.
10% de 675 ml
Passo 4: leite mais água mais óleo.
675 + 67,5 = 742,5 ml
Passo 5: quantidade de suco de laranja.
Para calcular a quantidade de suco de laranja, subtraímos o líquido que já somamos de 1000 ml.
1000 - 742,5 = 257,5 ml
Isadora precisa adicionar 257,5 ml de suco de laranja para completar a mistura no liquidificador até 1 litro.
Questão 3
Um tabuleiro quadrado é formado por 4 quadrados menores e deve ser preenchido com os números de 1 a 9, sem repetição.
Seja o tabuleiro representado da seguinte maneira:
![]()
Os números A, B, C e D são os valores que ocupam os quadrados menores.
Duas regras devem ser utilizadas para preencher o tabuleiro:
- a soma dos números nas diagonais devem ser iguais;
- em uma linha qualquer, uma potência deve ser formada utilizando um algarismo como base e o outro expoente. O resultado de ser o número de duas ordens formado na outra linha.
Uma possível solução para o tabuleiro é:
A) 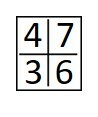
B) 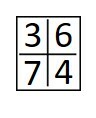
C) 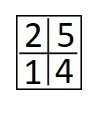
D) 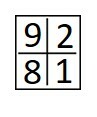
E) 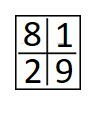
Aplicando a primeira regra, eliminamos as opções b e e, pois as diagonais somadas não apresentam resultados iguais.
Aplicando a segunda regra temos que na opção d, , o número formado pela outra linha.
Assim, a opção que satisfaz as duas regras é a d.
Questão 4
Carlos está organizando uma sequência de números ímpares consecutivos, começando pelo número 1, de forma que o primeiro termo seja 1, o segundo seja 3, o terceiro seja 5, e assim por diante. Ele quer saber qual será o 50º número da sequência.
A) 97
B) 99
C) 101
D) 103
E) 105
Carlos está organizando uma sequência de números ímpares, começando pelo número 1. A sequência fica assim:
1, 3, 5, 7, 9, 11, 13, 15, ...
Cada número da sequência aumenta 2 em relação ao anterior. Isso quer dizer que a cada novo número estamos "somando 2".
Veja que os números aumentam de 2 em 2: 1, 3, 5, 7, 9, e assim por diante.
Observe a posição e o número:
- O 1º número é 1.
- O 2º número é 3.
- O 3º número é 5.
- O 4º número é 7.
Percebemos que para qualquer posição, basta somar 2 repetidamente ao número anterior.
Conte até o 50º número:
- Já sabemos que a posição 1ª é o número 1.
- Cada posição seguinte, somamos 2.
Para simplificar, ao invés de somar 2 cinquenta vezes, podemos perceber que o 50º número terá 49 adições de 2, já que começamos com o número 1.
Calcule o 50º número:
Se a cada posição aumentamos 2, no 50º número teremos feito 49 somas de 2 a partir do número 1.
Vamos fazer a conta:
1+(49×2)=1+98=99
Então, o 50º número da sequência será 99.
Questão 5
Em uma escola, três professores combinaram que dariam aulas durante toda a manhã. O professor de Matemática ficou com das aulas, o professor de Português com
, e o professor de História com
do tempo total das aulas. Sabendo que o restante do tempo foi preenchido com atividades extras, qual fração do tempo foi dedicada às atividades extras?
A)
B)
C)
D)
E)
a) 1/12
b) 1/8
c) 1/4
d) 1/5
e) 1/6
Passo 1: identificar as frações de tempo dedicadas às aulas.
Cada professor ficou com uma parte do tempo total das aulas. Vamos usar frações para representar o tempo de cada um:
Professor de Matemática: Ficou com do tempo total das aulas.
Professor de Português: Ficou com do tempo total.
Professor de História: Ficou com 1/6 do tempo total.
Passo 2: somar as frações.
Para saber a fração total do tempo dedicado às aulas dos três professores, precisamos somar as frações:
Para somar frações, precisamos encontrar um denominador comum. O mínimo múltiplo comum (MMC) de 3, 4 e 6 é 12.
Agora, somamos:
Passo 3: Calcular a fração do tempo dedicada às atividades extras.
O tempo total das aulas é representado por 1 (ou ).
Se os professores usaram do tempo, o restante foi dedicado às atividades extras:
Simplificando:
A fração do tempo que foi dedicada às atividades extras é .
Questão 6
João escolheu um número inteiro, positivo e par. Ele somou a esse número os quatro números pares imediatamente superiores e os três números ímpares imediatamente inferiores, obtendo 2027 como resultado. Qual é a soma dos algarismos do número que João escolheu?
A) 5
B) 6
C) 7
D) 8
E) 9
Passo 1: entender o problema.
João escolheu um número inteiro positivo. Vamos chamá-lo de x. Ele fez o seguinte:
- Somou ao número x os quatro números pares imediatamente superiores.
- Somou também os três números ímpares imediatamente inferiores.
A soma de tudo isso resultou em 2027. Nosso objetivo é descobrir qual é o número x e, em seguida, somar os algarismos de x.
Passo 2: escrever a soma.
Vamos identificar os números que João usou na sua soma:
Número inicial: x.
Quatro números pares imediatamente superiores: x+2, x+4, x+6, e x+8.
Três números ímpares imediatamente inferiores: x−1, x−3, e x−5.
Assim, a soma fica:
x + (x + 2) + (x + 4) + (x + 6) + (x + 8) + (x - 1) + (x - 3) + (x - 5) = 2027
Passo 3: simplificar a expressão.
Somando todos esses termos, temos:
Passo 5: somar os algarismos de x.
O número que João escolheu foi 252. Somando os algarismos:
2 + 5 + 2 = 9
Conclusão:
A soma dos algarismos do número que João escolheu é 9.
Questão 7
Para mais questões da OBMEP:
- Questões para Olimpíada Mirim 1 OBMEP
- Questões para Olimpíada Mirim 2 OBMEP
- Questões para Olimpíada de Matemática OBMEP (6º e 7º ano do Fundamental II)
- Questões para Olimpíada de Matemática Nível 3 (ensino médio)
Veja também:
- 27 charadas de matemática com resposta
- 27 exercícios de Matemática Básica
- Exercícios de Raciocínio Lógico: 19 questões com respostas
- Teste de raciocínio lógico (com respostas e pontuação)
- Lógica Matemática
- Desafios matemáticos para estimular seu raciocínio
Referências Bibliográficas
OBMEP. Olimpíada Brasileira de Matemática das Escolas Públicas. Disponível em: http://www.obmep.org.br/. Acesso em: 24 out. 2024.
ASTH, Rafael. Questões para Olimpíada de Matemática (8º e 9º ano do Fundamental II). Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/questoes-para-olimpiadas-de-matematica-nivel-2/. Acesso em:


