A Matemática básica envolve os conteúdos estudados na escola no Ensino Fundamental e Médio, etapas que compõem a Educação Básica.
Desde o início do seu aprendizado, o aluno é apresentado aos campos da Matemática: Aritmética, Álgebra, Geometria, Estatística e Probabilidade.
A equivalência, ordem e a proporcionalidade são exemplos das ideias fundamentais que irão estar presentes em diversos assuntos dos campos da Matemática, portanto, nos exercícios.
Acompanhe a lista de exercícios de Matemática Básica com exercícios que selecionamos para você relembrar e desenvolver os conceitos básicos da Matemática. Todos os exercícios apresentam a resolução e explicação passo a passo para você tirar suas dúvidas.
Números (Aritmética)
Exercício 1 — Adição e Subtração
Na fazenda Morro Alto são produzidas laranjas. Assim que começou o período da colheita, uma grande produção já foi contabilizada. A tabela abaixo mostra a produção nos três primeiros dias.
a) Qual a produção total nos três primeiros dias?
b) De quanto foi a queda na produção entre o dia de maior e menor produção?
a)
O total da produção nos três dias foi de 10 379 laranjas.
b) 1 140 laranjas.
O dia de maior produção foi terça-feira, com 4 127 laranjas e, o de menor produção foi quarta-feira, com 2 987 laranjas. A diferença é o resultado da subtração entre estes valores.
Portanto, da terça-feira para quarta-feira houve uma queda na produção de 1 140 laranjas.
Exercício 2 - Multiplicação
Elisa está a procura de uma televisão para colocar em sua sala. Ela viu um anúncio de um modelo novo com as opções de pagamento à vista e a prazo.
Quanto Elisa pagará a mais se optar pelo pagamento a prazo?
Resposta: Pagará a mais R$ 306,00.
Estratégia: subtrair o total a prazo do preço à vista.
Total a prazo
Para o pagamento a prazo devemos multiplicar as parcelas para conhecer o total.
Diferença entre os dois valores
Portanto, optando pelo sistema a prazo, Elisa pagará R$ 306,00 a mais do que se optasse pelo sistema à vista.
Exercício 3 — Divisão
Em um projeto para a construção de um cinema, os arquitetos estão avaliando a relação entre a quantidade de fileiras e a quantidade de cadeiras em cada fileira. O projeto inicial prevê uma sala para 304 pessoas. No caso de utilizarem 19 fileiras, o número de cadeiras por fileira será
a) 14.
b) 15.
c) 16.
d) 13.
e) 12.
Resposta correta: c) 16.
Para determinar a quantidade de cadeiras por fileira devemos dividir a quantidade total de lugares no cinema, 304, pelo número de fileiras, 19.
Portanto, utilizando 19 fileiras, cada fileira terá 16 cadeiras.
Em uma gincana de férias, 75 crianças se inscreveram para participar das atividades de recreação. De modo a organizarem os jogos e atividades, eles verificaram a faixa etária dos inscritos e constataram que 2/5 das crianças têm mais de doze anos. Quantos participantes tem menos que 12 anos?
Resposta: 45 crianças.
Se 2/5 das crianças têm mais de 12 anos, 3/5 têm menos de 12 anos, pois
Para calcular quanto é 3/5 de 75, fazemos
Desta forma, 45 crianças têm menos de 12 anos.
Exercício 5 — Operações com Frações
Carlos, Roberto e Maurício são irmãos. Eles decidiram limpar e cortar a grama de um campinho de futebol que fica ao lado da casa deles para poderem brincar durante as férias. Até agora, Carlos e Roberto já limparam cada um uma parte.
Carlos que é o caçula limpou 1/5 do campo.
Roberto limpou 2/4 do campo.
Qual dos irmãos irá limpar a maior parte do campinho
Resposta: Roberto irá limpar a maior parte do campinho.
Resolução
Para determinar quem irá limpar a maior parte do campinho, devemos descobrir que parte Maurício irá limpar. Para comparar, as frações devem ter os mesmos denominadores.
Estratégia: subtrair da fração que representa o total da área do campinho, da fração (parte) que Carlos e Roberto já limparam, a parte que sobrar é a parte de Maurício.
Para somar as quantidades que Carlos e Roberto cortaram, devemos igualar os denominadores das frações. Para isso, determinamos o menor múltiplo comum entre 5 e 4 fazendo a fatoração.
O novo denominador das frações será, 20.
Para encontrar os numeradores das frações equivalentes, dividimos 20, que é o MMC, pelo denominador de cada fração original, e multiplicamos pelos numeradores.
A fração equivalente a de Carlos, será
Assim, o novo numerador será 4, e a fração será:
A fração equivalente a de Roberto, será
Assim, o novo numerador será 10, e a fração será:
Ao todo. Carlos e Roberto já cortaram
A fração que representa todo o campinho é 20/20
Desse modo, restam para Maurício limpar
Com as três frações com denominadores iguais, podemos comparar e descobrir de quem é a maior.
Assim, Roberto irá limpar a maior parte do campinho.
Em uma cidade são organizados a cada três anos os Jogos Universitários Gerais, um evento de competição esportiva que reúne os melhores nomes do esporte local. Em 2020 aconteceram os últimos jogos municipais, mesmo ano em que aconteceram os Jogos Olímpicos Internacionais, no Japão. Qual será o próximo ano em que os dois eventos irão acontecer simultaneamente?
Resposta: 2 032.
Os Jogos Olímpicos Internacionais acontecem a cada 4 anos e os Jogos Universitários Gerais a cada 3 anos. Escrevendo os anos em que acontecerão as próximas edições, temos:
Jogos Olímpicos: 2020, 2024, 2028, 2032
Jogos Universitários: 2020, 2023, 2026, 2029, 2032
Vemos que o próximo ano em que os dois eventos ocorrerão, simultaneamente, será 2032.
Para determinar este ano fazemos o Menor Mínimo Comum (MMC) entre 3 e 4, que são os intervalos de tempo para cada evento.
Para calcular o MMC, devemos fatorar 3 e 4, depois, multiplicamos os divisores.
Como o MMC entre 3 e 4 é 12, o próximo ano em que os dois eventos irão acontecer simultaneamente será:
Nossa herança genética pode trazer mais surpresas do que supomos. Uma árvore genealógica é um instrumento que permite registrar e organizar a história de nossos antepassados, nela a cada geração, desenhamos mais dois “galhos”.
Desta forma, a cada geração anterior, multiplicamos por dois o número de antepassados, em relação à anterior.
Se considerarmos uma média de vinte anos para cada geração como tempo médio para gerar novos descendentes, há duzentos anos, quantas pessoas estariam nomeadas em sua árvore genealógica, nesta geração específica?
Resposta: 1 024 antepassados.
Como estamos considerando 20 anos para cada geração, em 200 anos, teremos 10 gerações.
1ª geração passada: 2 pessoas (pais)
2ª geração passada: 4 pessoas (avós)
3ª geração passada: 8 pessoas (bisavós)
Queremos um modo de determinar quantos antepassados há em uma determinada geração. No caso da questão, a décima.
Fatorando as respostas para as primeiras 3 gerações, temos:
Expandindo este raciocínio, calculando uma potência de base 2, onde o expoente representa a geração que procuramos, determinamos a geração.
Desta forma, para a décima geração, temos:
Portanto, apenas na décima geração passada, havia 1 024 antepassados.
Exercício 8 — Números Decimais e Frações
Em uma corrida, quatro competidores disputam uma colocação nas finais do campeonato nacional. Em um determinado momento estas eram as frações que representavam o quanto cada atleta já havia percorrido da prova.
a) Na segunda posição, temos que os atletas A e D estão empatados, isso porque as frações 3/4 e 6/8 são equivalentes, representam a mesma quantidade, pois são frações equivaçentes.
Em relação ao primeiro colocado:
0,8 - 0,75 = 0,05
b) A prova completa é representada em fração, quando o numerador e igual ao denominador. Para cada atleta temos:
A loja Preço bom está vendendo um conjunto com 5 camisas por um preço promocional. Cada unidade sai por R$ 31,45 e o conjunto das cinco camisas sai pelo preço de quatro. Se optar pelo conjunto, o cliente pode dividir o valor em três vezes sem juros. De quanto será o preço da parcela?
Resposta: R$ 41,93.
O preço de quatro camisas:
Dividindo em três parcelas:
Sendo uma dízima periódica, faremos uma aproximação.
Se o período for maior que 5, aproximamos para 41,94.
Se o período for menor que 5, aproximamos para 41,93.
O período, parte que se repete, é 3. Como é menor que 5, aproximamos o preço da parcela para R$ 41,93.
Exercício 10 — Porcentagem, Juros simples e Compostos
Um investidor comprou R$ 18 000,00 em títulos do Tesouro Nacional. Os títulos que ele adquiriu são da modalidade pré-fixados, o que significa que o rendimento já é combinado na hora da compra. A taxa combinada foi de 0,08% a.m. (ao mês), considerando o sistema de juros simples.
Uma alternativa seria investir a mesma quantia em outros produtos financeiros no sistema de juros compostos.
Considerando 12 meses com a mesma quantia investida, caso o investidor optasse pelo sistema de juros compostos com a mesma taxa mensal, qual seria a diferença entre os montantes nos dois sistemas?
Resposta: A diferença será de R$ 78,10.
1º passo: conhecer o rendimento do investimento no sistema de juros simples, nos Títulos do Tesouro Nacional. Este rendimento são os juros.
Dados:
Sistema de juros simples;
Taxa (i): 0,8% ao mês = 0,008 ao mês
Tempo de investimento (t): 12 meses
O montante M, é o capital inicial investido C, mais os juros J.
M = C + J
Os juros por sua vez são a multiplicação entre o capital, a taxa e o tempo.
J = C.i.t
J = 18 000.0,008.12 = 1 728
O montante será:
M = 18 000 + 1 728 = 19 728
2º passo: conhecer o rendimento no sistema de juros compostos.
No sistema de juros compostos o montante é calculado como:
Substituindo os valores:
3° passo: calcular a diferença entre os montantes sob juros simples e compostos.
Exercício 11 — Equação do 1º grau com uma incógnita
Bianca aproveitou o domingo de Sol para passear com suas duas filhas. Ela comprou um sorvete para cada menina e uma garrafa de suco para ela que custava R$ 5,00. Ela pagou tudo com uma nota de R$ 50,00 e recebeu de troco R$ 36,00. Utilize uma equação para descrever esta situação, depois, determine o preço de cada sorvete.
Resposta: O sorvete custa R$ 4,50.
Chamando o preço do sorvete de x, temos que dois sorvetes serão 2x.
A equação fica da seguinte forma:
Para resolver uma equação do 1º grau, devemos isolar os termos com letras de um lado da igualdade.
Exercício 12 — Sistema de Equações do 1º grau com duas incógnitas
Um carro com flex consegue utilizar uma mistura de álcool e gasolina sem acarretar nenhum problema mecânico. Um condutor de um carro flex abasteceu 30 litros de combustível, misturando gasolina e álcool. Ele pagou um total de R$ 190,00. Neste posto, os preços da gasolina e do álcool são, respectivamente, R$ 8,00 e R$ 5,50. Quantos litros de cada combustível foram abastecidos?
Resposta: 10 litros de gasolina e 20 litros de álcool.
Quando temos dois valores desconhecidos, precisamos de duas equações para resolver um sistema.
Queremos saber quantos litros de álcool (a) e de gasolina (g) foram abastecidos.
Equação do preço
Equação da quantidade
Sabemos que o total de litros foi 30, dessa forma:
Utilizando o método da substituição, isolamos g na equação II.
g = 30 - a
Substituímos o valor de g, na equação I e resolvemos para a.
Assim, foram abastecidos 20 litros de álcool. Para determinar a quantidade de gasolina, basta substituir na equação II.
g + a = 30
g + 20 = 30
g = 30 - 20
g = 10
Portanto, 10 litros de gasolina foram abastecidos.
Exercício 13 — Equação do 2º grau
Um clube vai utilizar uma área quadrada para construir uma piscina de 12 m x 12 m. Ao redor da piscina será instalado um piso antiderrapante, como na ilustração.
No projeto inicial que o instalador recebeu, consta apenas a área a ser coberta com o piso antiderrapante, 52 m².
Sabendo que a largura de toda calçada ao redor da piscina se mantêm constante, qual a medida da largura desta calçada?
Considerando a área da piscina mais a área da calçada, temos:
Área da calçada = 52 m²
Área da piscina = 12 x 12 = 144 m²
Área total = 52 + 144 = 196 m²
Se olharmos para o quadrado exterior, da calçada, suas dimensões laterais são:
Medida do lado = x + 12 + x = 2x +12
A área total pode ser obtida pelo produto dos lados e, é igual a 196 m².
Usamos a propriedade distributiva da multiplicação para multiplicar todos os termos nos parênteses.
Juntando os termos semelhantes:
Trazendo 340 para o primeiro membro da equação:
Para determinar a largura x da calçada, devemos resolver a equação do segundo grau, isto é, determinar suas raízes.
Uma equação do segundo grau tem a forma .
Os termos desta equação do segundo grau são:
a = 4
b = 48
c = -52
Como todos os coeficientes são divisíveis por 4, podemos simplificar a equação:
a = 4 / 4 = 1
b = 48 / 4 = 12
c = -52 / 4 = -13
O discriminante (delta) da equação é igual a:
Utilizando a Fórmula de Bhaskara:
Substituindo os valores:
Como se trata de uma medida, descartamos a raiz x1, pois é negativa.
Uma marca de óculos está avaliando a possibilidade de abrir uma nova fábrica e, para isto, está analisando os custos de fabricação por quantidade de óculos produzidos. Após um levantamento com fornecedores, a marca conseguiu baratear ao máximo o custo das matérias-primas e uma unidade sairá por R$ 8,50.
Além dos custos por unidade, existem os custos fixos como: aluguel, salários, energia e impostos. O total destes valores é de R$ 20 000,00 por mês.
a) Escreva a lei de uma função que relaciona o capital necessário para produzir uma quantia de x unidades.
b) Esboce o gráfico desta função.
c) Se 1 000 óculos forem produzidos, qual o preço mínimo que eles precisam ser vendidos para se pagar pelo menos os custos, sem acarretar lucro nem prejuízo ao fabricante.
a) C(x) = 20 000 + 8,5x
b)
O gráfico mostra que mesmo para nenhum óculos produzido o custo é de R$ 20 000. A partir daí, o custo aumenta de forma linear, a uma taxa de R$ 8,50 por óculos produzido.
c) R$ 28,50.
Passo 1: calcular o custo para produzir 1 000 óculos.
Substituindo na função, o custo para fabricar 1 000 óculos é de:
Passo 2: calcular o preço de cada óculos para que o custo seja pago.
Portanto, para que o custo se pague, será preciso vender os 1 000 óculos, por R$ 28,50 cada.
Exercício 15 — Razão, Grandezas Proporcionais e Regra de Três
Com a chegada do verão os clubes com piscina se preparam para receber muitos associados aos finais de semana. Em um clube foi realizada uma manutenção na piscina principal que possui a capacidade de 86 400 L, por isso teve de ser esvaziada. O tempo para enche-la com a vazão habitual é de três dias, mas como o clube está com urgência, a vazão será aumentada em seis vezes. Em quanto tempo a piscina estará cheia?
Resposta: a piscina estará cheia em 12 h com a nova vazão.
Com a vazão habitual, 86 400 L são enchidos em três dias, ou, 72 h.
24 x 3 = 72
A vazão é:
Aumentando a vazão em seis vezes, está será de:
1 200 x 6 = 7 200 L / h
Pela propriedade fundamental das proporções, multiplicando cruzado:
Portanto, a piscina estará cheia em 12 h com a nova vazão.
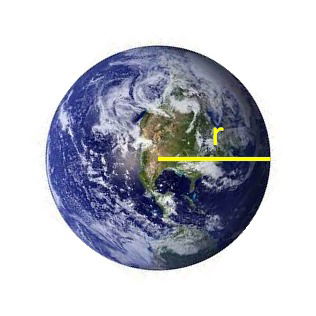
O Planeta Terra possui um raio de cerca de 6 371 km. Se considerarmos a Terra como uma esfera perfeita qual o comprimento de sua circunferência. Considere .
O comprimento de uma circunferência é calculado pela relação:
Substituindo os valores, temos:
Este é um valor aproximado pois, o número é irracional, por isso possui infinitas casas decimais e, estamos considerando apenas as duas primeiras casas após a vírgula.
Exercício 17 — Soma das medidas dos ângulos internos de um triângulo
Na figura, determine a medida do ângulo , sabendo que o segmento é perpendicular a .
Resposta: O ângulo mede 101°.
A soma dos ângulos internos de um triângulo é igual a 180º. Dessa forma, no triângulo ABD temos:
53° + 90° + x = 180°
x = 180° - 90° - 53°
x = 37°
No triângulo BDC, temos:
90° + 26° + y = 180°
y = 180° - 90° - 26°
y = 64°
Portanto, a medida do ângulo é:
Exercício 18 — Geometria Analítica, Distância entre dois pontos.
Determine a distância entre os pontos A e B.
Resposta: 4,74 unidades de comprimento.
Para determinar a distância entre quaisquer dois pontos no plano cartesiano, utilizamos o Teorema de Pitágoras.
Utilizando o Teorema de Pitágoras que diz: " O quadrado da hipotenusa é igual a soma dos quadrados dos catetos".
Onde a hipotenusa é h e os catetos são:
5 - 1 = 4
e
2 - 1 = 1
Sendo assim, a distância entre os pontos A e B é . Aproximando a raiz quadrada temos: 4,12 unidades de comprimento.
Três bolas de beisebol estão embaladas em um cilindro, perfeitamente ajustadas, sem se deformarem. As bolas de beisebol, que possuem um diâmetro de 7,6 cm tocam as superfícies internas do cilindro nas laterais e nas bases.
Determine o volume do espaço vazio que sobra dentro do cilindro. Considere .
Resposta: o volume é de, aproximadamente 329 cm³.
O espaço vazio é o volume do cilindro menos os volumes das bolas.
Espaço vazio = volume do cilindro - 3x volume de uma bola
1º passo: determinar o raio e a altura do cilindro.
Raio: como o diâmetro do cilindro coincide com o diâmetro das bolas de beisebol, o raio do cilindro também é o mesmo das bolas.
raio = diâmetro / 2
raio = 7,6 / 2 = 3,8 cm
Altura: a altura do cilindro é igual a três diâmetros das bolas.
altura do cilindro = 3 x diâmetro de uma bola.
altura do cilindro = 3 x 7,6 = 22,8 cm
2º passo: determinar o volume do cilindro.
Volume do cilindro = área da base vezes a altura
Como a base é uma circunferência, sua área é:
Dessa forma, o volume do cilindro é:
Substituindo os valores
3º passo: calcular o volume das esferas.
Substituindo os valores:
Como são três bolas:
3 x 219,488 = 658,464 cm³
4º passo: subtrair do volume do cilindro, o volumes das bolas.
Espaço vazio = volume do cilindro - volume das bolas
Espaço vazio = 987,696 cm³ - 658,464 cm³
Espaço vazio = 329,232 cm³
Desta forma, o espaço vazio que sobra no cilindro é de, aproximadamente, 329 cm³.
Exercício 20 — Teorema de Tales
As retas r, s e t são paralelas. Determine a medida do segmento x no triângulo.
Rersposta: 37,5.
Os segmentos e do triângulo são concorrentes e são cortados por retas paralelas. De acordo com o Teorema de Tales, quando retas concorrentes são cortadas por retas paralelas, são formados segmentos proporcionais.
"Multiplicando cruzado", propriedade fundamental das proporções:
Exercício 21 — Retas paralelas cortadas por uma transversal
As retas r e s são paralelas entre si, assim como, q e p também. Determine e justifique as medidas dos ângulos desconhecidos.
Os ângulos azul e verde são suplementares, somados formam 180°. Desta forma, chamando o valor do ângulo azul de x, temos:
150° + x = 180°
x = 180° - 150° = 30°
Ângulo azul = 30°
Os ângulos verde e rosa são alternos externos, por isso são iguais.
Ângulo rosa = 150°
Os ângulos amarelo e rosa são suplementares. Chamando o valor do ângulo amarelo de y, temos:
Em determinada hora do dia, uma árvore faz uma sombra de comprimento igual a 50 m e um ângulo de 30° com o chão. Determine a altura da árvore e a hipotenusa do triângulo.
Conteúdo: a altura da árvore é de, aproximadamente, 28,83 m.
Altura da árvore
Podemos determinar a altura da árvore utilizando a tangente do ângulo de 30°, que diz que:
A tangente é igual a divisão entre a medida do cateto oposto e o cateto adjacente.
Os catetos são os lados do triângulo que formam o ângulo de 90°, e a altura da árvore é o cateto oposto ao ângulo de 30°.
Chamando a altura da árvore de a, temos:
De uma tabela trigonométrica, temos que a tangente do ângulo de 30° é igual a:
Substituindo o valor da tangente de 30° na relação I, temos:
Usando a propriedade fundamental das proporções, multiplicamos cruzado.
Aproximando o valor da raiz de três para 1,73:
A altura da árvore é de, aproximadamente, 28,83 m.
Exercício 23 - Trigonometria
Determine as medidas dos segmentos BC e CA.
No triângulo ABC, 50 m é a medida da hipotenusa. Podemos determinar as medidas dos segmentos BC, que é o cateto adjacente ao ângulo de 60°, e do cateto oposto ao ângulo de 60°, que é o segmento AC.
Cálculo do segmento AC.
O seno do ângulo de 60° é igual a divisão da medida do cateto oposto pela medida da hipotenusa.
De uma tabela trigonométrica, temos que o valor do seno de 60° é .
Substituindo os valores:
Portanto, o comprimento do lado AC é de m.
Cálculo do segmento BC.
O segmento BC pode ser calculado pelo cosseno do ângulo de 60°, sendo a divisão entre BC e a hipotenusa.
De uma tabela trigonométrica temos que o cosseno do ângulo de 60° vale .
Os jogos de cartas de baralho são muito populares. Os baralhos consistem em um conjunto de 52 cartas, divididas em conjuntos menores de 13 cartas chamados naipes: paus, espadas, copas e ouros. Retirando uma carta ao acaso, qual a probabilidade de não ser uma carta do naipe de paus.
Retirar uma carta ao acaso é um experimento aleatório em que o espaço amostral é equiprovável. Isso quer dizer que toda carta tem a mesma chance de ser "sorteada", tem a mesma probabilidade.
A probabilidade é calculada como a razão entre o número favorável ao evento e o número total de elementos do espaço amostral.
O evento é: não ser uma carta de paus. Vamos chamar de evento A.
Neste caso, estamos interessados na probabilidade de sair:
52 - 13 = 39
Assim, das 52 cartas do baralho, 39 não são de paus.
A probabilidade de ocorrer o evento A, é de:
Em porcentagem, 75%.
Portanto, a probabilidade de não ser uma carta do naipe de paus é 75%.
Exercício 25 — Probabilidade e gráfico de setores
Uma pesquisa realizada com 100 jovens de idades entre 20 e 25 anos em um Campus Universitário levantou os seguintes dados em relação a massa corporal dos entrevistados:
A pesquisa ainda aponta que, dos jovens com peso ideal, 37% praticam regularmente algum tipo de atividade física.
Ao sortear um dos cem jovens entrevistados ao acaso, qual a probabilidade dele estar com peso ideal e ainda praticar esportes?
Verificando a parte verde do gráfico, vemos que 47% dos jovens estão no peso ideal.
Destes, 37% praticam atividade física. Queremos determinar quanto é 37% de 47%.
Em porcentagem, 17,39%.
Exercício 26 — Estatística: Moda, Mediana, Média Aritmética
Em um processo seletivo oito concorrentes realizaram um teste e obtiveram os seguintes resultados.
Pedro
8
Jéssica
7
Augusto
9
Fernando
4
Manoel
6
Bia
3
Kássia
6
Nicole
8
Em relação aos resultados, determine:
a) A moda.
b) A mediana.
c) A média aritmética.
a) As modas são: 6 e 8.
Moda é o/os valores que mais se repetem. Nesse caso, dois valores se repetem mais de uma vez, o 6 e o 8.
Observação: um conjunto sem valores repetidos é chamado de amodal.
b) A mediana é 6,5.
Para determinar a mediana devemos colocar os dados em ordem crescente ou decrescente. A esta ordenação damos o nome de ROL de dados.
Se o conjunto de dados tiver um número par de elementos, a mediana será a média aritmética entre os dois valores centrais.
Se o conjunto de dados possuir um número ímpar de elementos, a mediana será exatamente o elemento do centro.
c) A média aritmética é 6,375
Para calcular a média aritmética, somamos todos os valores e dividimos pelo número total de elementos.
Exercício 27 — Estatística
Uma pesquisa realizada com 120 alunos de uma escola de Ensino Fundamental, levantou o tempo que eles ficavam expostos à telas, como celulares e tablets.
Com base nos dados da pesquisa determine:
a) A frequência absoluta de crianças na faixa de 120 a 180 minutos por dia.
b) A frequência relativa de alunos na faixa dos 60 a 90 minutos por dia.
c) Qual porcentagem dos alunos ficam até 90 minutos por dia expostos à telas.
a) A frequência absoluta é 16.
Frequência absoluta (Fa) é a quantidade de cada variável. Neste caso, o número de crianças que passam entre 120 e 180 minutos usando aparelhos digitais.
O total de 120 representa a soma de todas as frequências absolutas.
Chamando de x o valor desconhecido temos:
b) A frequência relativa é 12,5%
A frequência relativa é a divisão entre a frequência absoluta de uma variável e o total. Neste caso, a divisão entre o número de alunos na faixa entre sessenta e noventa minutos, que é 15, e o total, 120.
c) 31,6% dos alunos ficam até 90 min por dia no celular ou tablet.
Até 90 minutos engloba as duas primeiras faixas. O total de alunos nas duas primeiras faixas é de:
23 + 15 =38
Dos 120 alunos, 38 estão nas duas faixas.
Em porcentagem, 31,6%.
Veja mais exercícios de Probabilidade e Estatística
Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
.
.
é irracional, por isso possui infinitas casas decimais e, estamos considerando apenas as duas primeiras casas após a vírgula.
, sabendo que o segmento 
é perpendicular a 
.
. Aproximando a raiz quadrada temos: 4,12 unidades de comprimento.
.
e 
do triângulo são concorrentes e são cortados por retas paralelas. De acordo com o Teorema de Tales, quando retas concorrentes são cortadas por retas paralelas, são formados segmentos proporcionais.
.
m.
.
