Exercícios de seno, cosseno e tangente
Estude com os exercícios de seno, cosseno e tangente resolvidos. Pratique e tire suas dúvidas com os exercícios comentados.
Questão 1
Determine os valores de x e y no triângulo a seguir. Considere sen 37º = 0,60, cosseno de 37º = 0,79 e tan 37º = 0,75.
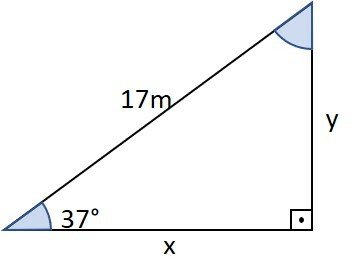
Questão 2
No triângulo retângulo a seguir, determine o valor do ângulo , em graus, e seu seno, cosseno e tangente.
Considere:
sen 28º = 0,47
cos 28º = 0,88
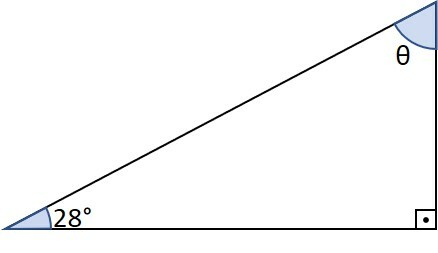
Questão 3
Em uma determinada hora de um dia ensolarado, a sombra de uma casa se projeta por 23 metros. Esta sobra faz 45º em relação ao solo. Desta forma, determine a altura da casa.
Questão 4
Um agrimensor é um profissional que utiliza conhecimentos matemáticos e geométricos para fazer medições e estudar uma superfície. Utilizando um teodolito, ferramenta que, entre outras funções mede ângulos, posicionado a 37 metros de distância de um edifício, ele encontrou um ângulo de 60° entre um plano paralelo ao solo e altura do edifício. Se o teodolito estava sobre um tripé, a 180 cm do chão, determine a altura do edifício em metros.
Considere
Questão 5
Determine o perímetro do pentágono.
Considere:
sen 67° = 0,92
cos 67° = 0,39
tan 67° = 2,35
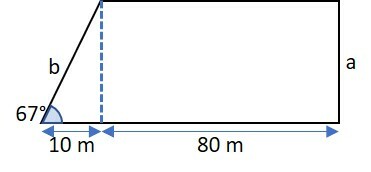
Questão 6
Determine o seno e o cosseno de 1 110°.
Questão 7
(CEDERJ 2021) Estudando para uma prova de trigonometria, Júlia aprendeu que sen² 72° é igual a
1 – cos² 72°.
cos² 72° – 1.
tg² 72° – 1.
1 – tg² 72º.
A relação fundamental da trigonometria diz que:
Onde x é o valor do ângulo.
Fazendo x = 72º e isolando o seno, temos:
Questão 8
(USF 2017) As rampas são uma boa forma de assegurar a acessibilidade para cadeirantes e indivíduos com mobilidade reduzida. A acessibilidade a edificações, mobiliário, espaços e equipamentos urbanos é assegurada em lei.
A Associação Brasileira de Normas Técnicas (ABNT), de acordo com a Lei Brasileira de Inclusão da Pessoa com Deficiência (13.146/2015), regula a construção e define a inclinação das rampas, bem como os cálculos para a sua construção. As diretrizes de cálculo da ABNT, indicam um limite máximo de inclinação de 8,33% (proporção de 1:12). Isso significa que uma rampa, para vencer um desnível de 1 m, deve ter, no mínimo, 12 m de comprimento e isso define que o ângulo de inclinação da rampa, em relação ao plano horizontal, não pode ser maior que 7°.
De acordo com as informações anteriores, para que uma rampa, com comprimento igual a 14 m e inclinação de 7º em relação ao plano, esteja dentro das normas da ABNT, ela deve servir para vencer um desnível com altura máxima de
Use: sen 7º = 0,12; cos 7º = 0,99 e tg 7º = 0,12.
a) 1,2 m.
b) 1,32 m.
c) 1,4 m.
d) 1,56 m.
e) 1,68 m.
A rampa forma um triângulo retângulo onde o comprimento é de 14 m, fazendo um ângulo de 7º em relação à horizontal, onde a altura é o cateto oposto ao ângulo.
Utilizando seno de 7°:
A altura que a rampa deve vencer é de 1,68 m.
Questão 9
(Unesp 2012) Um prédio hospitalar está sendo construído em um terreno declivoso. Para otimizar a construção, o arquiteto responsável idealizou o estacionamento no subsolo do prédio, com entrada pela rua dos fundos do terreno. A recepção do hospital está 5 metros acima do nível do estacionamento, sendo necessária a construção de uma rampa retilínea de acesso para os pacientes com dificuldades de locomoção. A figura representa esquematicamente esta rampa (r), ligando o ponto A, no piso da recepção, ao ponto B, no piso do estacionamento, a qual deve ter uma inclinação α mínima de 30º e máxima de 45º.
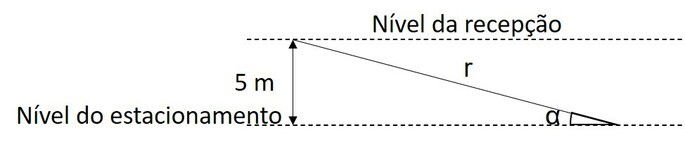
Nestas condições e considerando , quais deverão ser os valores máximo e mínimo, em metros, do comprimento desta rampa de acesso?
Questão 10
(EPCAR 2020) À noite, um helicóptero da Força Aérea Brasileira sobrevoa uma região plana e avista um VANT (Veículo Aéreo Não Tripulado) de forma circular e altura desprezível, com raio de 3 m estacionado paralelamente ao solo a 30 m de altura.
O VANT está a uma distância y metros de um holofote que foi instalado no helicóptero.
O feixe de luz do holofote que ultrapassa o VANT incide sobre a região plana e produz uma sombra circular de centro O e raio R.
O raio R da circunferência da sombra forma um ângulo de 60º com o feixe de luz, conforme se vê na figura seguinte.
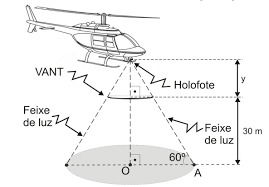
Nesse momento, uma pessoa que se encontra num ponto A da circunferência da sombra corre para o ponto O, pé da perpendicular traçada do holofote à região plana.
A distância, em metros, que essa pessoa percorre de A até O é um número entre
a) 18 e 19
b) 19 e 20
c) 20 e 21
d) 22 e 23
Objetivo
Determinar o comprimento do segmento , raio da circunferência da sombra.
Dados
- Altura de O até o VANT é de 30 m.
- O raio do VANT é de 3 m.
Utilizando a tangente de 60° determinamos a parte destacada em vermelho na seguinte imagem:
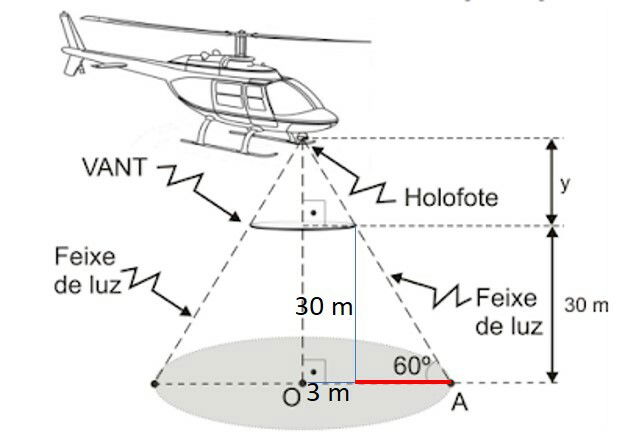
Considerando a tangente de 60° = e sendo a tangente a razão entre o cateto oposto ao ângulo e seu adjacente, temos:
Racionalizando
O comprimento AO é
Aproximando o valor de
A medida aproximada do segmento AO é de 20,3 m, ou seja, um valor entre 20 e 21.
Questão 11
Continue praticando com:
- Exercícios de trigonometria no triângulo retângulo
- Exercícios de Trigonometria
- Índices de exercícios de matemática do 1º ano do Ensino Médio
- Exercícios sobre razões trigonométricas
- Exercícios sobre funções trigonométricas
Leia também:
- Seno, Cosseno e Tangente
- Trigonometria no Triângulo Retângulo
- Trigonometria
- Relações Métricas no Triângulo Retângulo
- Relações Trigonométricas
- Funções Trigonométricas
- Os assuntos mais difíceis do 1º ano do Ensino Médio (e como dominá-los)
ASTH, Rafael. Exercícios de seno, cosseno e tangente. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-de-seno-cosseno-e-tangente/. Acesso em:


