Busque um tema

Língua Portuguesa
Biologia
Matemática
História
Geografia
ENEM
Exercícios
Mais Matérias
Corretor de Redação Enem

Toda Matéria
Exercícios
›
Exercícios de Matemática

Exercícios de trigonometria no triângulo retângulo

Rafael C. Asth

Professor de Matemática e Física

A trigonometria é um importante tema na Matemática que possibilita conhecer lados e ângulos em um triângulo retângulo, através do seno, cosseno e tangente, além de outras funções trigonométricas.

Para melhorar nos estudos e ampliar seus conhecimentos, acompanhe a lista de 8 exercícios, mais 4 questões de vestibulares, todas resolvidas passo a passo.

Exercício 1

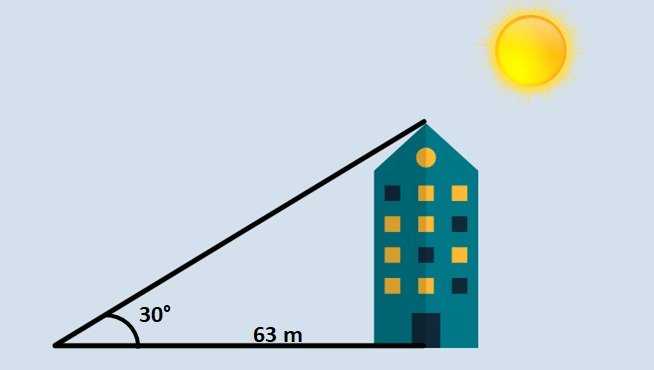
Observando pela manhã a sombra de um prédio no chão, uma pessoa verificou que essa media 63 metros quando os raios de Sol faziam um ângulo de 30° com a superfície. Baseado nessas informações, calcule a altura do prédio.

figura mostrando sombra de um prédio no chão que mede 63 m quando os raios de Sol fazem um ângulo de 30º

Ver Resposta

Resposta correta: Aproximadamente 36,37 m.

O prédio, a sombra e o raio de Sol, determinam um triângulo retângulo. Utilizando o ângulo de 30° e a tangente, podemos determinar a altura do prédio.

$tan g e n t e espaço igual a espaço numerador c a t e t o espaço o p o s t o sobre denominador c a t e t o espaço a d j a c e n t e fim da fração$

Sendo h a altura do prédio, temos:

$tan espaço 30 sinal de grau espaço igual a espaço h sobre 63 espaço espaço h espaço igual a espaço 63 espaço sinal de multiplicação espaço tan espaço 30 sinal de grau espaço espaço espaço h espaço igual a espaço 63 espaço sinal de multiplicação espaço numerador raiz quadrada de 3 sobre denominador 3 fim da fração h espaço igual a espaço 21 raiz quadrada de 3 espaço m h espaço aproximadamente igual espaço 36 vírgula 37 espaço m$

Exercício 2

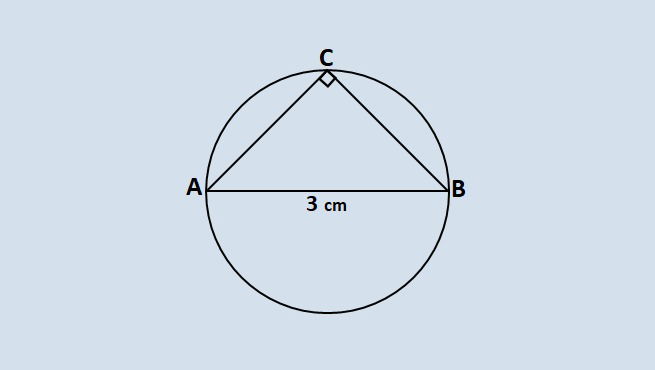
Em uma circunferência de diâmetro igual a 3, um segmento AC, chamado de corda, forma um ângulo de 90° com outra corda CB, de mesmo comprimento. Qual é a medida das cordas?

Ver Resposta

Resposta correta: O comprimento da corda é 2,12 cm.

Como os segmentos AC e CB formam um ângulo de 90° e possuem o mesmo comprimento, o triângulo formado é isósceles e os ângulos da base são iguais.

Como a soma dos ângulos internos de um triângulo é igual a 180º e, já temos um ângulo de 90°, sobram outros 90° para serem divididos igualmente entre os dois ângulos da base. Assim, o valor desses é igual 45º cada.

Sendo o diâmetro igual a 3 cm, o raio vale 1,5 cm e podemos utilizar o cosseno de 45° para determinar o comprimento da corda.

$cos espaço 45 sinal de grau espaço igual a espaço numerador 1 vírgula 5 sobre denominador c o r d a fim da fração c o r d a espaço igual a espaço numerador 1 vírgula 5 sobre denominador cos espaço 45 sinal de grau fim da fração c o r d a espaço igual a espaço numerador 1 vírgula 5 sobre denominador começar estilo mostrar numerador raiz quadrada de 2 sobre denominador 2 fim da fração fim do estilo fim da fração c o r d a espaço igual a espaço 1 vírgula 5 espaço sinal de multiplicação espaço numerador 2 sobre denominador raiz quadrada de 2 fim da fração c o r d a espaço aproximadamente igual 2 vírgula 12 espaço c m$

Exercício 3

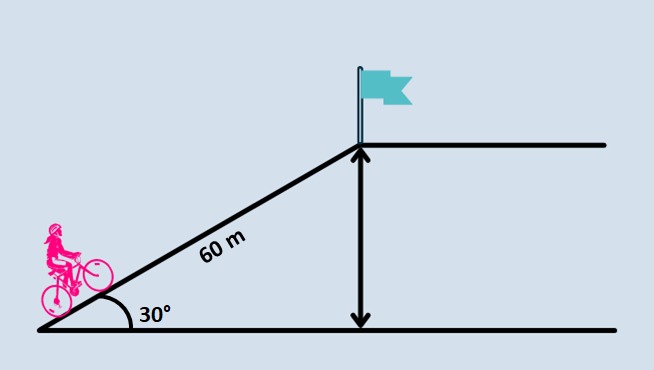
Uma ciclista participando de um campeonato se aproxima da linha de chegada que se encontra no alto de uma ladeira. O comprimento total dessa última parte da prova é de 60 m e o ângulo formado entre a rampa e a horizontal é de 30°. Sabendo disso, calcule a altura vertical que a ciclista precisa subir.

Ver Resposta

Resposta correta: A altura será de 30 m.

Chamando a altura de h, temos:

$s e n espaço 30 º espaço igual a espaço numerador h espaço sobre denominador 60 fim da fração espaço h espaço igual a espaço 60 espaço sinal de multiplicação espaço s e n 30 sinal de grau espaço h espaço igual a espaço 60 espaço sinal de multiplicação espaço 1 meio h espaço igual a espaço 30 espaço m$

Exercício 4

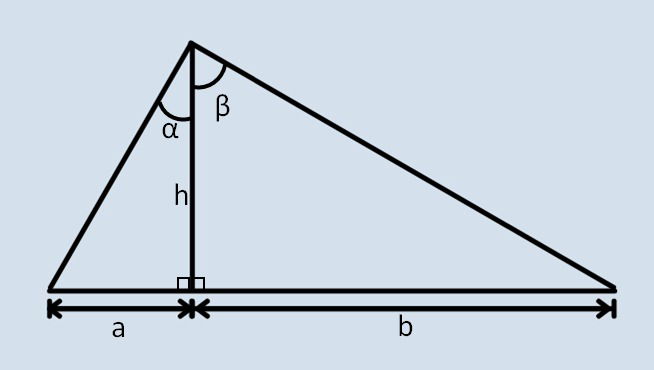
A seguinte figura é formada por três triângulos onde a altura h determina dois ângulos retos. Os valores dos elementos são:

α = 30°
β = 60°
h = 21

Determine o valor de a+b.

Ver Resposta

Resposta correta:

$28 raiz quadrada de 3$

Podemos determinar as medidas dos segmentos a e b, utilizando as tangentes dos ângulos fornecidos.

Cálculo de a:

$tan espaço alfa espaço igual a espaço a sobre h espaço espaço a espaço igual a espaço h espaço sinal de multiplicação espaço tan espaço alfa espaço espaço a espaço igual a espaço 21 espaço sinal de multiplicação espaço numerador raiz quadrada de 3 sobre denominador 3 fim da fração a espaço igual a 7 raiz quadrada de 3$

Cálculo de b:

$tan espaço beta espaço igual a espaço numerador b espaço sobre denominador h espaço fim da fração b espaço igual a espaço h espaço sinal de multiplicação espaço tan espaço beta b espaço igual a espaço 21 espaço sinal de multiplicação espaço raiz quadrada de 3 b espaço igual a 21 raiz quadrada de 3$

Assim,

$a espaço mais espaço b espaço igual a espaço 28 raiz quadrada de 3$

Exercício 5

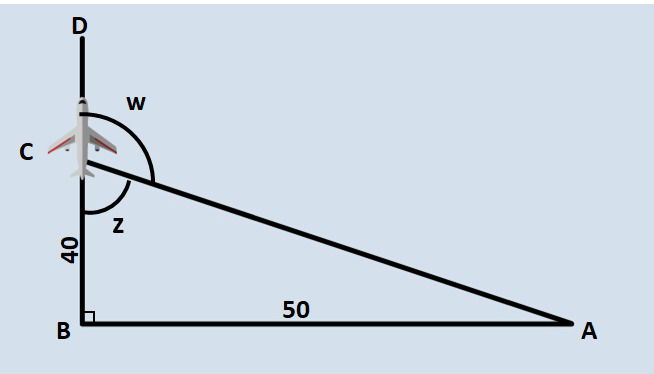
Um avião decolou da cidade A e voou 50 km em linha reta até pousar na cidade B. Após, voou mais 40 km, dessa vez indo na direção da cidade D. Essas duas rotas fazem um ângulo de 90° entre si. No entanto, devido às condições climáticas desfavoráveis, o piloto recebeu um comunicado da torre de comando informando que não poderia pousar na cidade D e, que deveria voltar para a cidade A.

Para que fizesse o retorno a partir do ponto C, o piloto deveria fazer uma curva de quantos graus à direita?

Considere:

sen 51° = 0,77
cos 51° = 0,63
tan 51° = 1,25

Ver Resposta

Resposta correta: O piloto deve realizar uma curva de 129° à direita.

Analisando a figura vemos que o trajeto forma um triângulo retângulo.

Vamos chamar o ângulo que estamos procurando de W. Os ângulos W e Z são suplementares, ou seja, formam um ângulo raso, de 180°.

Assim, W + Z = 180°.

W = 180 - Z (equação 1)

Nossa tarefa agora é determinar o ângulo Z e, para isso, vamos utilizar a sua tangente.

$tan espaço Z espaço igual a espaço 50 sobre 40 tan espaço Z espaço igual a espaço 1 vírgula 25$

Devemos nos perguntar: Qual é o ângulo cuja tangente é 1,25?

O problema nos fornece esse dado, tan 51° = 1,25.

Esse valor também pode ser encontrado em uma tabela trigonométrica ou com uma calculadora científica, utilizando a função:

$tan à potência de menos 1 fim do exponencial$

Substituindo o valor de Z na equação 1, temos:

W = 180° - 51° = 129°

Exercício 6

Um raio de luz monocromática ao passar de um meio para outro, sofre um desvio em sua direção. Essa mudança na sua propagação está relacionada aos índices de refração dos meios, conforme a seguinte relação:

Lei de Snell - Descartes

$s e n espaço r espaço x espaço n com 2 subscrito espaço igual a espaço s e n espaço i espaço x espaço n com 1 subscrito$

Sendo i e r os ângulos de incidência e refração e, n1 e n2, os índices de refração dos meios 1 e 2.

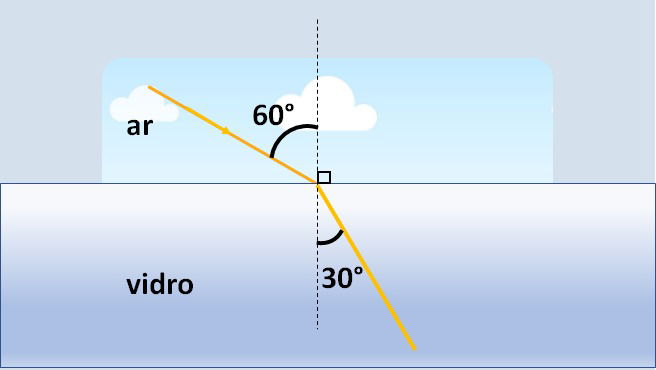
Ao incidir na superfície de separação entre o ar e o vidro, um raio de luz altera sua direção, como mostra a figura. Qual o índice de refração do vidro?

Dado: Índice de refração do ar igual a 1.

Ver Resposta

Resposta correta: O índice de refração do vidro é igual a $raiz quadrada de 3$ .

Substituindo os valores temos:

$s e n espaço 30 sinal de grau espaço sinal de multiplicação espaço n com v i d r o subscrito fim do subscrito espaço igual a espaço espaço n com a r subscrito fim do subscrito espaço sinal de multiplicação espaço s e n espaço 60 sinal de grau espaço n com v i d r o subscrito fim do subscrito espaço igual a numerador espaço n com a r espaço subscrito fim do subscrito sinal de multiplicação espaço s e n espaço 60 sinal de grau sobre denominador s e n espaço 30 sinal de grau fim da fração n com v i d r o subscrito fim do subscrito espaço igual a espaço numerador 1 espaço sinal de multiplicação começar estilo mostrar numerador raiz quadrada de 3 sobre denominador 2 fim da fração fim do estilo sobre denominador começar estilo mostrar 1 meio fim do estilo fim da fração n com v i d r o subscrito fim do subscrito espaço igual a espaço numerador raiz quadrada de 3 sobre denominador 2 fim da fração espaço sinal de multiplicação espaço 2 sobre 1 espaço igual a espaço raiz quadrada de 3$

Exercício 7

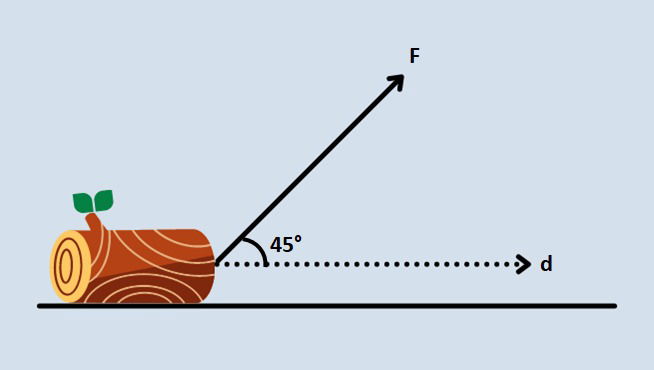
Para arrastar uma tora de madeira até sua oficina, um serralheiro amarrou uma corda a tora e a puxou por três metros através de uma superfície horizontal. Uma força de 40 N através da corda fez um ângulo de 45° com o sentido do deslocamento. Calcule o trabalho da força aplicada.

Ver Resposta

Resposta correta: O trabalho realizado é de, aproximadamente, 84,85 J.

O trabalho é uma grandeza escalar obtida pelo produto entre a força e o deslocamento. Se a força não possui a mesma direção do deslocamento, devemos decompor está força e considerar apenas a componente nesta direção.

Nesse caso, devemos multiplicar o módulo da força pelo cosseno do ângulo.

Assim temos:

$T espaço igual a espaço F espaço. espaço d espaço. espaço cos espaço 45 sinal de grau T espaço igual a espaço 40 espaço. espaço 3 espaço. espaço numerador raiz quadrada de 2 sobre denominador 2 fim da fração T espaço igual a espaço 60 espaço. espaço raiz quadrada de 2 T espaço aproximadamente igual espaço 84 vírgula 85 espaço J$

Exercício 8

Entre duas serras, os moradores de dois vilarejos tinham que percorrer um duro caminho de descida e subida. Para resolver a situação, foi decidido que uma ponte estaiada seria construída entre os vilarejos A e B.

Seria preciso calcular a distância entre os dois vilarejos pela linha reta em que a ponte seria esticada. Como os moradores já conheciam a altura das cidades e os ângulos de subida, essa distância poderia ser calculada.

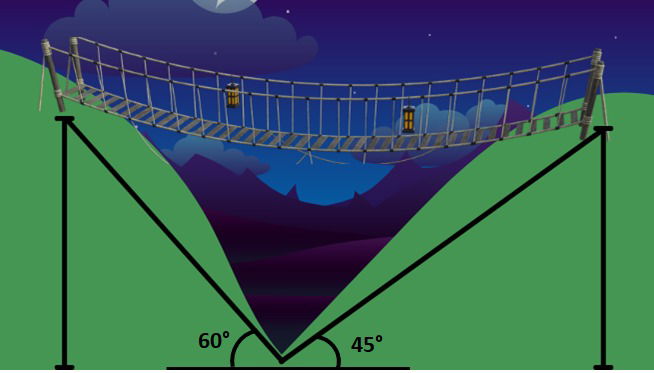
Com base no esquema abaixo e sabendo que a altura das cidades era de 100 m, calcule o comprimento da ponte.

Ver Resposta

Resposta correta: A ponte deve possuir um comprimento de, aproximadamente, 157,73 m.

O comprimento da ponte é a soma dos catetos adjacentes aos ângulos fornecidos. Chamando a altura de h, temos:

Cálculo com o ângulo de 45°

$tan espaço 45 sinal de grau espaço igual a espaço numerador h sobre denominador c a t e t o espaço a d j a c e n t e fim da fração c a t e t o espaço a d j a c e n t e espaço igual a espaço numerador h sobre denominador tan espaço 45 sinal de grau fim da fração c a t e t o espaço a d j a c e n t e espaço igual a espaço numerador 100 sobre denominador começar estilo mostrar 1 fim do estilo fim da fração c a t e t o espaço a d j a c e n t e espaço igual a 100 espaço m$

Cálculo com o ângulo de 60°

$tan espaço 60 sinal de grau espaço igual a espaço numerador h sobre denominador c a t e t o espaço a d j a c e n t e fim da fração c a t e t o espaço a d j a c e n t e espaço igual a espaço numerador h sobre denominador tan espaço 60 sinal de grau fim da fração c a t e t o espaço a d j a c e n t e espaço igual a espaço numerador 100 sobre denominador começar estilo mostrar raiz quadrada de 3 fim do estilo fim da fração c a t e t o espaço a d j a c e n t e espaço aproximadamente igual espaço 57 vírgula 73 espaço m$

Para determinar o comprimento da ponte, somamos os valores obtidos.

c o m p r i m e n t o espaço igual a espaço 100 espaço mais espaço 57 vírgula 73 espaço aproximadamente igual espaço 157 vírgula 73 espaço m

Questão 1

Cefet - SP

No triângulo ABC abaixo, CF = 20 cm e BC = 60 cm. Assinale as medidas dos segmentos AF e BE respectivamente.

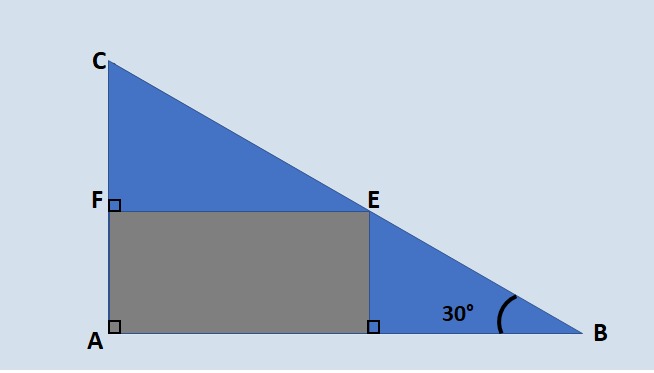
a) 5, 15
b) 10, 20
c) 15, 25
d) 20, 10
e) 10, 5

Ver Resposta

Resposta: b) 10, 20

Para determinar AF

Notamos que AC = AF + CF, assim temos que:

AF = AC - CF (equação 1)

CF é fornecido pelo problema, sendo igual a 20 cm.

AC pode ser determinado utilizando o seno de 30°.

$s e n espaço 30 sinal de grau espaço igual a espaço numerador A C sobre denominador B C fim da fração espaço A C espaço igual a espaço B C espaço sinal de multiplicação espaço s e n espaço 30 sinal de grau espaço$

BC é fornecido pelo problema, sendo igual a 60 cm.

$A C espaço igual a espaço 60 espaço sinal de multiplicação espaço 1 meio igual a espaço 30 espaço c m.$

Substituindo na equação 1, temos:

$A F espaço igual a espaço A C espaço menos espaço C F espaço espaço A F espaço igual a espaço 30 espaço menos espaço 20 espaço igual a espaço 10 espaço c m$

Para determinar BE

Primeira observação:

Verificamos que a figura dentro do triângulo é um retângulo, devido aos ângulos retos determinados na figura.

Sendo assim, seus lados são paralelos.

Segunda observação:

O segmento BE forma um triângulo retângulo com um angulo de 30° onde: a altura é igual a AF, que acabamos de determinar e, BE é a hipotenusa.

Fazendo o cálculo:

Utilizamos o seno de 30° para determinar BE

$s e n espaço 30 sinal de grau espaço igual a espaço numerador 10 sobre denominador B E fim da fração espaço espaço B E espaço igual a espaço numerador 10 sobre denominador s e n espaço 30 sinal de grau fim da fração espaço B E espaço igual a espaço numerador 10 sobre denominador começar estilo mostrar 1 meio fim do estilo fim da fração B E espaço igual a espaço 20 espaço c m$

Questão 2

EPCAR-MG

Um avião decola de um ponto B sob inclinação constante de 15° com a horizontal. A 2 km de B se encontra a projeção vertical C do ponto mais alto D de uma serra de 600 m de altura, conforme a figura.

Dados: cos 15° = 0,97; sen 15° = 0,26; tg 15° = 0,27

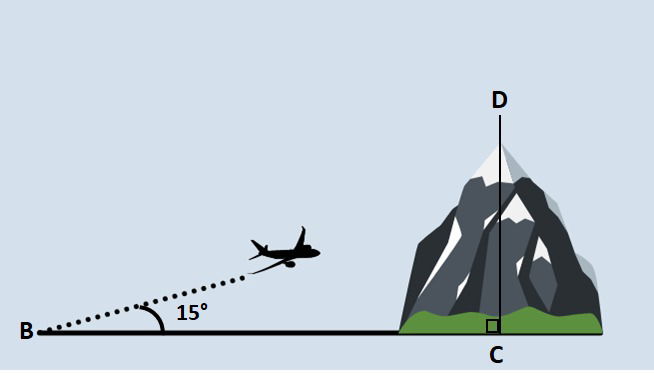
É correto afirmar que:

a) Não haverá colisão do avião com a serra antes de alcançar 540 m de altura.
b) Haverá colisão do avião com a serra em 540 m de altura.
c) Haverá colisão do avião com a serra em D.
d) Se o avião decolar 220 m antes de B, mantendo a mesma inclinação, não haverá colisão do avião com a serra.

Ver Resposta

Resposta: b) Haverá colisão do avião com a serra em 540 m de altura.

Em primeiro lugar é necessário utilizar o mesmo múltiplo da unidade de medida de comprimento. Sendo assim, passaremos 2 km para 2000 m.

Seguindo as mesmas condições iniciais de voo, podemos prever a altura em que o avião estará na projeção vertical do ponto C.

Utilizando a tangente de 15° e definindo como h a altura, temos:

$tan espaço 15 sinal de grau espaço igual a espaço numerador h espaço sobre denominador 2000 fim da fração espaço h espaço igual a espaço 2000 espaço sinal de multiplicação espaço tan espaço 15 º espaço espaço h espaço igual a espaço 2000 espaço sinal de multiplicação espaço 0 vírgula 27 espaço espaço espaço h espaço igual a espaço 540 espaço m$

Questão 3

ENEM 2018

Para decorar um cilindro circular reto será usada uma faixa retangular de papel transparente, na qual está desenhada em negrito uma diagonal que forma 30° com a borda inferior. O raio da base do cilindro mede 6/π cm, e ao enrolar a faixa obtém-se uma linha em formato de hélice, como na figura.

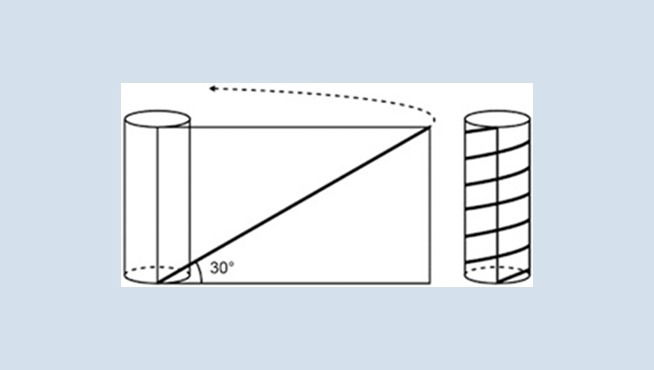
O valor da medida da altura do cilindro, em centímetro, é:

a) 36√3
b) 24√3
c) 4√3
d) 36
e) 72

Ver Resposta

Resposta: b) 24√3

Observando a figura notamos que foram dadas 6 voltas ao redor do cilindro. Como é um cilindro reto, em qualquer parte da sua altura teremos uma circunferência como a base.

Para calcular a medida da base do triângulo.

O comprimento de uma circunferência pode ser obtido pela fórmula:

Sendo r o raio e, igual a $tipográfico 6 sobre reto pi$ ,temos:

$2 espaço. espaço reto pi espaço. espaço espaço 6 sobre reto pi$

Como são 6 voltas:

$6 espaço. espaço 2 espaço. espaço reto pi espaço. espaço 6 sobre reto pi espaço igual a espaço 72 espaço$

Podemos usar a tan de 30° para calcular a altura.

$tan espaço 30 sinal de grau espaço igual a espaço numerador a l t u r a espaço sobre denominador b a s e fim da fração espaço espaço a l t u r a espaço igual a espaço b a s e espaço sinal de multiplicação espaço tan espaço 30 sinal de grau espaço a l t u r a espaço igual a espaço 72 espaço sinal de multiplicação espaço numerador raiz quadrada de 3 sobre denominador 3 fim da fração a l t u r a espaço igual a espaço 24 raiz quadrada de 3$

Questão 4

ENEM 2017

Raios de luz solar estão atingindo a superfície de um lago formando um ângulo X com a sua superfície, conforme indica a figura.

Em determinadas condições, pode-se supor que a intensidade luminosa desses raios, na superfície do lago, seja dada aproximadamente por I(x) = k . sen(x), sendo k uma constante, e supondo-se que X está entre 0° e 90º.

Quando x = 30º, a intensidade luminosa se reduz a qual percentual de seu valor máximo?

A) 33%
B) 50%
C) 57%
D) 70%
E) 86%

Ver Resposta

Resposta: B) 50%

Substituindo o valor de seno de 30° na função, obtemos:

$I parêntese esquerdo x parêntese direito espaço igual a espaço k espaço. espaço s e n espaço 30 sinal de grau I parêntese esquerdo x parêntese direito espaço igual a espaço k espaço. espaço 1 meio$

Tendo reduzido o valor de k a sua metade, a intensidade é de 50%.

Pratique mais exercícios em:

Exercícios de trigonometria
Exercícios sobre razões trigonométricas
Exercícios sobre funções trigonométricas com respostas
Índice de exercícios de matemática do 1º ano do Ensino Médio.

Amplie seus conhecimentos com:

Trigonometria no triângulo retângulo
Exercícios sobre Teorema de Pitágoras
Relações Métricas no Triângulo Retângulo
Trigonometria

Rafael C. Asth

Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.

ASTH, Rafael. Exercícios de trigonometria no triângulo retângulo. Toda Matéria, [s.d.]. Disponível em: https://www.todamateria.com.br/exercicios-de-trigonometria-no-triangulo-retangulo-comentados/. Acesso em:

Veja também