🚀 60% OFF para turbinar seus estudos! Assine agora
Acelere seu aprendizado
ASSINAR TM +

Exercícios sobre álgebra linear (com respostas resolvidas)

Rafael C. Asth
Rafael C. Asth
Professor de Matemática e Física

Pratique exercícios sobre álgebra linear com matrizes e vetores. Tire suas dúvidas com as resoluções passo a passo.

Exercício 1

Considere o seguinte sistema linear:

abre chaves atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com 3 x espaço mais espaço 2 y espaço igual a espaço 7 fim da célula linha com célula com x espaço menos espaço y espaço igual a espaço 2 fim da célula fim da tabela fecha

Utilizando o método de eliminação de Gauss para resolver este sistema, qual é o par ordenado (x, y) que satisfaz ambas as equações?

a) (1/5, -1/5)

b) (2, 0)

c) (3, -1/5)

d) (11/5, 1/5)

e) (3, -2)

Gabarito explicado

Vamos resolver o sistema utilizando o método de eliminação de Gauss.

Passo 1: Escrevemos o sistema na forma de matriz aumentada:

abre colchetes tabela linha com 3 2 célula com linha vertical 7 fim da célula linha com 1 célula com menos 1 fim da célula célula com linha vertical 2 fim da célula fim da tabela fecha colchetes

Passo 2: Transformamos o elemento (2,1) em zero, subtraindo da segunda linha o produto da primeira linha por 1/3:

Nova linha 2 = Linha 2 - (1/3) × Linha 1

Nova Linha 2 = [1, -1, 2] - (1/3) × [3, 2, 7]

Nova Linha 2 = [1, -1, 2] - [1, 2/3, 7/3]

Nova Linha 2 = [0, -5/3, -1/3]

A matriz agora fica:

abre colchetes tabela linha com 3 2 célula com linha vertical 7 fim da célula linha com 0 célula com menos 5 sobre 3 fim da célula célula com espaço linha vertical menos 1 terço fim da célula fim da tabela fecha colchetes

Passo 3: Escalonamento. Multiplicamos a segunda linha por -3/5 para obter o coeficiente 1 para y:

Nova linha 2 = (-3/5) × Linha 2

Nova Linha 2 = (-3/5) × [0, -5/3, -1/3]

Nova Linha 2 = [0, 1, 1/5]

A matriz agora fica:

abre colchetes tabela linha com 3 2 célula com linha vertical 7 fim da célula linha com 0 1 célula com espaço linha vertical 1 quinto fim da célula fim da tabela fecha colchetes

Passo 4: Substituição para encontrar o valor da variável x:

Da segunda equação, temos: y = 1/5

Substituindo este valor na primeira equação:

3 x espaço mais espaço 2 y espaço igual a espaço 73 x espaço mais espaço 2.1 quinto espaço igual a espaço 73 x espaço mais espaço 2 sobre 5 espaço igual a espaço 73 x igual a espaço 7 menos 2 sobre 53 x igual a espaço 35 sobre 5 menos 2 sobre 53 x igual a espaço 33 sobre 5x igual a espaço numerador 33 sobre denominador 5.3 fim da fraçãox igual a espaço 33 sobre 15x igual a espaço 11 sobre 5

Portanto, a solução do sistema é x = 11/5 e y = 1/5.

Exercício 2

Seja a matriz A igual a abre colchetes tabela linha com 3 célula com menos 1 fim da célula 4 linha com 2 0 5 fim da tabela fecha colchetes e B igual a abre colchetes tabela linha com 1 2 linha com célula com menos 3 fim da célula 4 linha com 0 célula com menos 1 fim da célula fim da tabela fecha colchetes .Calcule parêntese esquerdo A vezes B parêntese direito à potência de T e escolha a alternativa correta:

a) abre colchetes tabela linha com 5 17 linha com 10 19 fim da tabela fecha colchetes espaço

b) abre colchetes tabela linha com célula com espaço espaço espaço 6 fim da célula célula com espaço espaço espaço 2 fim da célula linha com célula com menos 2 fim da célula célula com menos 1 fim da célula fim da tabela fecha colchetes

c) abre colchetes tabela linha com 5 10 linha com 17 27 fim da tabela fecha colchetes

d) abre colchetes tabela linha com 3 14 linha com 8 17 fim da tabela fecha colchetes

e) abre colchetes tabela linha com 7 15 linha com 9 21 fim da tabela fecha colchetes

Gabarito explicado

Primeiro, vamos calcular o produto A ⋅ B:

A ⋅ B = abre colchetes tabela linha com 3 célula com menos 1 fim da célula 4 linha com 2 0 5 fim da tabela fecha colchetes espaço. espaço abre colchetes tabela linha com 1 2 linha com célula com menos 3 fim da célula 4 linha com 0 célula com menos 1 fim da célula fim da tabela fecha colchetes

Para calcular cada elemento do produto, usamos a multiplicação de linhas por colunas:

c11 = 3⋅1 + (−1)⋅(−3) + 4⋅0 = 3+3+0 = 6

c12 = 3⋅2 + (−1)⋅4 + 4⋅(−1) = 6−4−4 = −2

c21 = 2⋅1 + 0⋅(−3) + 5⋅0 = 2+0+0 = 2

c22 = 2⋅2 + 0⋅4 + 5⋅(−1) = 4+0−5 = −1

Portanto:

A vezes B igual a abre colchetes tabela linha com 6 célula com menos 2 fim da célula linha com 2 célula com menos 1 fim da célula fim da tabela fecha colchetes

Agora, calculamos a transposta do produto parêntese esquerdo A vezes B parêntese direito à potência de T:

Para essa transformação, cada linha se transformará em coluna.

abre parênteses A vezes B fecha parênteses à potência de T igual a abre colchetes tabela linha com célula com espaço espaço espaço 6 fim da célula célula com espaço espaço espaço 2 fim da célula linha com célula com menos 2 fim da célula célula com menos 1 fim da célula fim da tabela fecha colchetes

Resposta correta: opção b.

Exercício 3

Dada a matriz A abaixo, reduza-a à sua forma escalonada utilizando o método de Gauss-Jordan:

A igual a abre colchetes tabela linha com 1 2 célula com menos 1 fim da célula linha com 2 1 célula com espaço espaço 3 fim da célula linha com célula com menos 1 fim da célula célula com espaço 3 espaço espaço fim da célula célula com espaço espaço 2 fim da célula fim da tabela fecha colchetes

Escolha a matriz escalonada reduzida correta:

a)

b)

c)

d)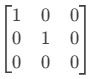

e)

Gabarito explicado

Passo 1: Escreva a matriz aumentada (se aplicável) ou a matriz original.

abre colchetes tabela linha com 1 2 célula com menos 1 fim da célula linha com 2 1 célula com espaço espaço 3 fim da célula linha com célula com menos 1 fim da célula célula com espaço 3 espaço espaço fim da célula célula com espaço espaço 2 fim da célula fim da tabela fecha colchetesA igual a abre colchetes tabela linha com 1 2 célula com menos 1 fim da célula linha com 2 1 célula com espaço espaço 3 fim da célula linha com célula com menos 1 fim da célula célula com espaço 3 espaço espaço fim da célula célula com espaço espaço 2 fim da célula fim da tabela fecha colchetes

Passo 2: Eliminação para forma escalonada (Gauss).

  • Subtraia 2×Linha 1 da Linha 2:

L2←L2−2L1

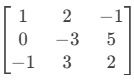
  • Some Linha 1 à Linha 3:

L3←L3+L1

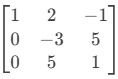
  • Divida Linha 2 por -3:

L2← numerador 1 sobre denominador menos 3 fim da fração. L 2

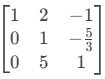
  • Subtraia 5×Linha 2 da Linha 3:

L3←L3−5L2

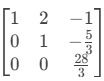
Ao final desta etapa, já temos o matriz na forma escalonada, no entanto, vamos reescrevê-la na forma reduzida.

Passo 3: Redução para forma escalonada reduzida (Gauss-Jordan).

  • Divida Linha 3 por 28 sobre 3

L3←28 sobre 3L3

  • Some 5 sobre 3× Linha 3 à Linha 2:

L2←L2+5 sobre 3L3

  • Some Linha 3 à Linha 1 e subtraia 2×Linha 2 da Linha 1:

L1←L1+L3−2L2

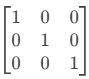
A forma escalonada reduzida de A é a matriz identidade, pois o sistema é possível e determinado.

Exercício 4

Considere o vetor v com seta para a direita sobrescrito igual a parêntese esquerdo 3 vírgula 4 parêntese direito no plano cartesiano. Qual é o ângulo θ que este vetor forma com o eixo x positivo?

a) 30°

b) 45°

c) 53,13°

d) 60°

e) 36,87°

Gabarito explicado

Para encontrar o ângulo que um vetor forma com o eixo x positivo, podemos utilizar a fórmula:

teta igual a a r c tan abre parênteses y sobre x fecha parênteses

Onde:

  • x é a componente horizontal do vetor;
  • y é a componente vertical do vetor.

No nosso caso, temos o vetor v com seta para a direita sobrescrito igual a parêntese esquerdo 3 vírgula 4 parêntese direito, portanto:

x=3

y=4

Substituindo na fórmula:

teta igual a a r c tan abre parênteses 4 sobre 3 fecha parênteses

Calculando este valor:

teta igual a a r c tan abre parênteses 4 sobre 3 fecha parênteses espaço aproximadamente igual 53 vírgula 13 º

Exercício 5

Conteúdo exclusivo para assinantes Toda Matéria+
Além de mais exercícios, tenha acesso a mais recursos para dar um up nos seus estudos.
Corretor de Redação para o Enem
Exercícios exclusivos
Estude sem publicidade
Assinar Toda Matéria+

Veja também:

Rafael C. Asth
Rafael C. Asth
Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também
Leitura Recomendada
Tópicos Relacionados
Exercícios Exercícios de Matemática Matemática Álgebra
Que tal um up?
Toda Matéria+
Corretor de Redação
para o Enem Ferramenta Inteligente com feedback instantâneo
Exercícios exclusivos Acesso a centenas de questões com gabaritos
Estude sem publicidade Navegação limpa e focada para evitar distrações
Assinar Toda Matéria+
Toda Matéria no YouTube
Thumbnail Toda Matéria no Youtube
Toda Matéria Inscreva-se