Teorema de Tales - Exercícios

Rafael C. Asth
Rafael C. Asth
Professor de Matemática e Física

O teorema de Tales indica que quando um feixe de retas paralelas são cortadas por duas retas transversais, formam segmentos proporcionais.

Aproveite a lista de exercícios resolvidos e comentados para tirar todas as suas dúvidas sobre esse importante teorema da geometria.

Questão 1

As retas t, u e v são paralelas. Determine o valor da medida do segmento x.

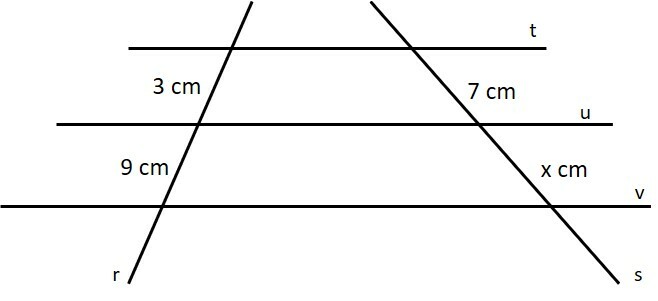
Retas paralelas cortadas por transversais.

Resposta: 21 cm.

Utilizando o Teorema de Tales, podemos escrever uma proporção entre os segmentos.

3 sobre 9 igual a 7 sobre reto x 3 reto x igual a 7.9 3 reto x igual a 63 reto x igual a 63 sobre 3 reto x igual a 21 espaço cm

Questão 2

Sabendo que as retas r, s e t são paralelas, determine o valor de x na imagem a seguir.

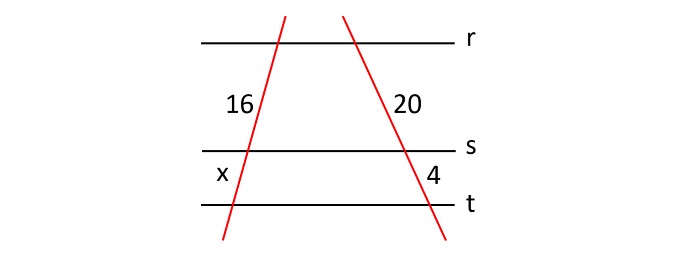
Exercício sobre o teorema de Tales

Resposta correta: 3,2.

Pelo teorema de Tales, temos que:

20 sobre 4 igual a 16 sobre reto x

Utilizando a propriedade fundamental das proporções e multiplicando meios pelos extremos, encontramos o valor de x.

20 reto x espaço igual a espaço 64 reto x espaço igual a espaço 64 sobre 20 reto x espaço igual a espaço 3 vírgula 2

Portanto, o valor de x é 3,2.

Questão 3

João decidiu dividir um terreno, conforme a imagem abaixo.

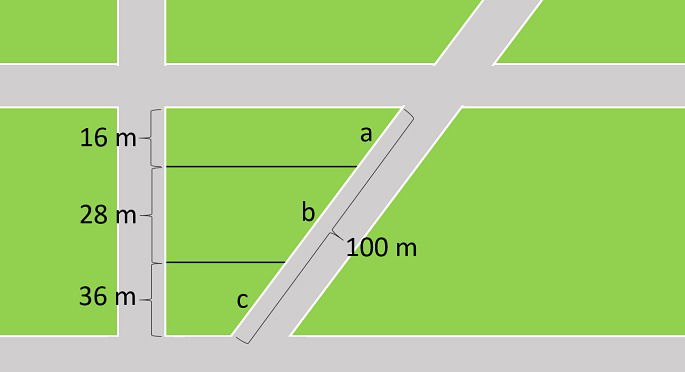
Exercício sobre o teorema de Tales

Com base nos dados apresentados, os valores de a, b e c são, respectivamente:

a) 10 m, 15 m e 20 m
b) 20 m, 35 m e 45 m
c) 30 m, 45 m e 50 m
d) 15 m, 25 m e 35 m

Resposta correta: b) 20 m, 35 m e 45 m.

Como sabemos o comprimento de a + b + c, podemos fazer as seguintes relações para encontrar o valor de a:

numerador 16 sobre denominador 16 espaço mais espaço 28 espaço mais espaço 36 fim da fração igual a numerador reto a sobre denominador reto a espaço mais espaço reto b espaço mais espaço reto c fim da fração 16 sobre 80 igual a reto a sobre 100

Utilizando a propriedade fundamental das proporções e multiplicando meios pelos extremos, encontramos o valor de a.

16.100 espaço igual a espaço 80. reto a 1600 espaço igual a espaço 80 reto a reto a espaço igual a espaço numerador 1600 espaço sobre denominador 80 fim da fração reto a igual a espaço 20

Para encontrar o valor de b realizamos o mesmo raciocínio.

numerador 28 sobre denominador 28 espaço mais espaço 36 fim da fração igual a numerador reto b sobre denominador 100 espaço menos espaço reto a fim da fração numerador 28 sobre denominador 28 espaço mais espaço 36 fim da fração igual a numerador reto b sobre denominador 100 espaço menos espaço 20 fim da fração 28 sobre 64 igual a reto b sobre 80 28.80 espaço igual a espaço 64. reto b 2240 espaço igual a espaço 64 reto b reto b espaço igual a espaço 2240 sobre 64 reto b espaço igual a espaço 35

E, por fim, calculamos o valor de c.

numerador 36 sobre denominador 28 espaço mais espaço 16 fim da fração igual a numerador reto c sobre denominador reto a espaço mais espaço reto b fim da fração 36 sobre 44 igual a numerador reto c sobre denominador 20 espaço mais espaço 35 fim da fração 36 sobre 44 igual a reto c sobre 55 36.55 espaço igual a espaço 44. reto c 1980 espaço igual a espaço 44 reto c reto c espaço igual a espaço 1980 sobre 44 reto c espaço igual a espaço 45

Portanto, os valores de a, b e c são, respectivamente, 20 m, 35 m e 45 m.

Questão 4

Existem 5 bolas dispostas em uma mesa de bilhar. A reta formada entre as bolas 1 e 2 é paralela à reta formada entre as bolas 4 e 5.

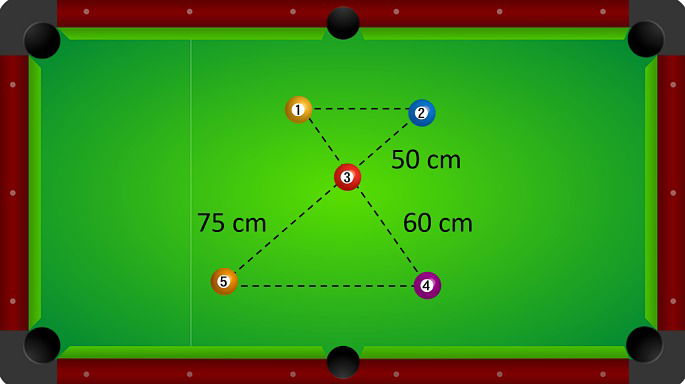
Exercício sobre o teorema de Tales

De acordo com as medidas dispostas na imagem responda: qual a distância entre as bolas 1 e 3?

a) 20 cm
b) 30 cm
c) 40 cm
d) 50 cm

Resposta correta: c) 40 cm.

Substituindo os valores apresentados na imagem no teorema de Tales, temos:

75 sobre 50 espaço igual a espaço 60 sobre reto x 75 reto x espaço igual a espaço 50.60 75 reto x espaço igual a espaço 3000 reto x espaço igual a espaço 3000 sobre 75 reto x espaço igual a espaço 40

Portanto, a bola 1 está a 40 cm de distância da bola 3.

Questão 5

Um triângulo ADE foi projetado em cima do triângulo ABC, conforme a imagem a seguir.

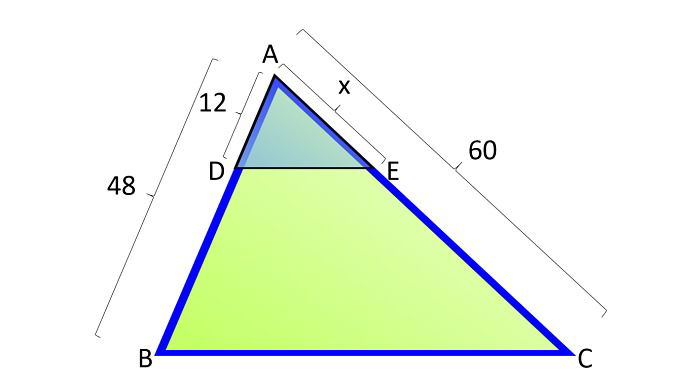
Exercício sobre o teorema de Tales

Com base nos dados apresentados encontre o valor de x.

Resposta correta: x = 15.

Substituindo no teorema de Tales os valores dados na imagem, temos:

AD sobre AB igual a AE sobre AC 12 sobre 48 igual a x sobre 60 48 x igual a 60.12 48 x igual a 720 x igual a 720 sobre 48 reto x espaço igual a espaço 15

Portanto, o valor de x é 15.

Veja também: Teorema de Tales

Questões de Concurso Resolvidas

Questão 6

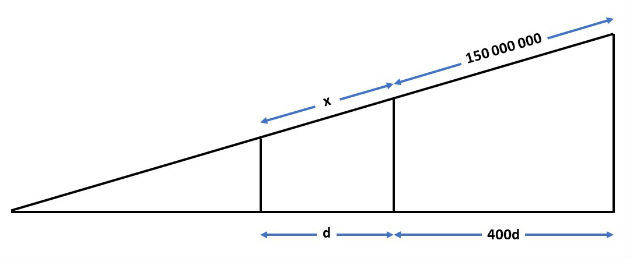
(Cefet/MG - 2017) A figura a seguir é um esquema representativo de um eclipse lunar em que a Lua, a Terra e o Sol estão representados pelas circunferências de centros C1, C2 e C3, respectivamente, que se encontram alinhados. Considera-se que a distância entre os centros da Terra e do Sol é 400 vezes maior que a distância entre os centros da Terra e da Lua e que a distância do ponto T na superfície da Terra ao ponto S na superfície do Sol, como representados na figura, é de 150 milhões de quilômetros.

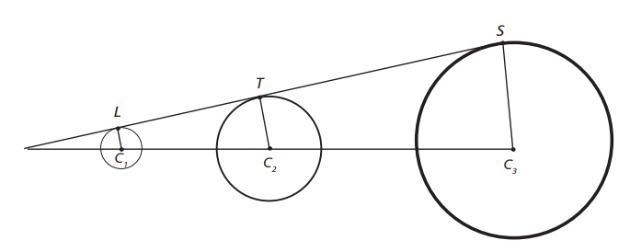
Questão cefet/mg 2017 teorema de tales

Sabendo-se que os segmentos de reta começar estilo tamanho matemático 14px C com 1 subscrito L em moldura superior fecha moldura vírgula espaço C com 2 subscrito T em moldura superior fecha moldura vírgula espaço C com 3 subscrito S em moldura superior fecha moldura fim do estilo são paralelos, a distância do ponto L, representado na superfície da Lua, ao ponto T, na superfície da Terra, é igual a

a) 375.000 Km.
b) 400.000 Km.
c) 37.500.000 Km.
d) 40.000.000 Km.

Alternativa correta: a) 375.000 Km.

A situação pode ser representada conforme a figura abaixo:

Questão cefet-mg 2017 Teorema de Tales

Como os segmentos de reta tamanho 14px C com tamanho 14px 1 subscrito tamanho 14px L em moldura superior fecha moldura tamanho 14px vírgula tamanho 14px espaço tamanho 14px C com tamanho 14px 2 subscrito tamanho 14px T em moldura superior fecha moldura tamanho 14px vírgula tamanho 14px espaço tamanho 14px C com tamanho 14px 3 subscrito tamanho 14px S em moldura superior fecha moldura são paralelos, pelo teorema de Tales temos a seguinte proporção:

Alternativa: a) 375.000 Km.

Questão 7

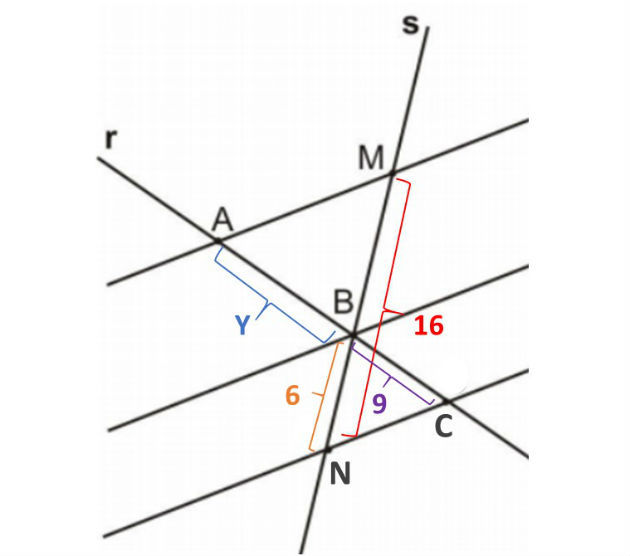
(Epcar - 2018) Observe a figura a seguir:

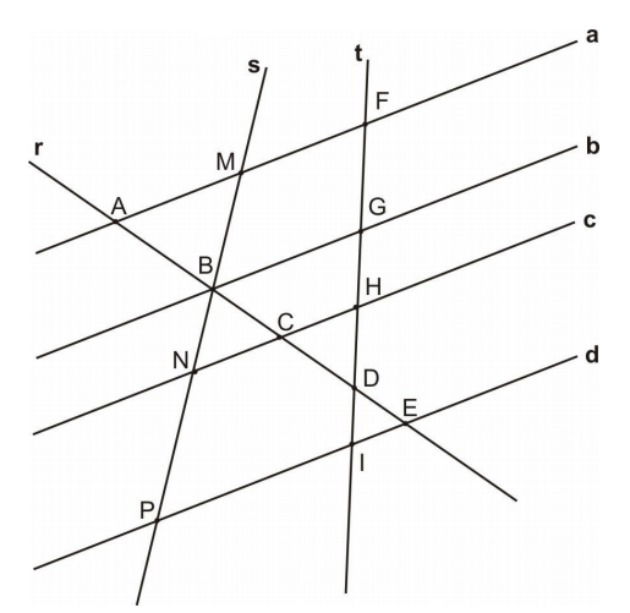
Questão Epcar 2018 Teorema de Tales

Nela, as retas a, b, c e d são paralelas e são interceptadas pelas retas transversais r, s e t.

Assim, as medidas dos segmentos, em cm, são:

A B em moldura superior fecha moldura igual a y espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço B C em moldura superior fecha moldura igual a 9 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço C D em moldura superior fecha moldura igual a 10 D E em moldura superior fecha moldura igual a 4 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço F G em moldura superior fecha moldura igual a z espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço G H em moldura superior fecha moldura igual a m H D em moldura superior fecha moldura igual a 5 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço D I em moldura superior fecha moldura igual a 2 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço M N em moldura superior fecha moldura igual a 16 B N em moldura superior fecha moldura igual a 6 espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço B P em moldura superior fecha moldura igual a x espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço espaço

A soma começar estilo tamanho matemático 14px AB em moldura superior mais F H em moldura superior fecha moldura fim do estilo , em cm, é dada por um número divisível por

a) 3
b) 4
c) 7
d) 11

Alternativa correta: a) 3

Observando a imagem, identificamos que:

A B em moldura superior fecha moldura mais F H em moldura superior fecha moldura igual a y mais z mais m

Para encontrar esses valores, vamos separar na figura os segmentos proporcionais e aplicar o teorema de Tales.

Iniciaremos calculando o valor de y. Para tal, assinalamos os valores conhecidos, conforme indicado abaixo:

Questão Epcar 2018 teorema de tales

Observando a figura, notamos que:

B M em moldura superior fecha moldura igual a M N em moldura superior fecha moldura menos B N em moldura superior fecha moldura B M em moldura superior fecha moldura igual a 16 menos 6 igual a 10 espaço c m

Aplicando o teorema de Tales:

y sobre 9 igual a 10 sobre 6 y igual a numerador 9.10 sobre denominador 6 fim da fração igual a 15 espaço c m

Para encontrar o valor de m, vamos utilizar a seguinte proporção:

Questão Epcar 2018 teorema de tales

5 sobre 10 igual a m sobre 9 m igual a numerador 9.5 sobre denominador 10 fim da fração m igual a 9 sobre 2 c m

Agora que conhecemos o valor do m, podemos encontrar o valor de z usando a seguinte proporção:

Questão Epcar 2018 teorema de tales

6 sobre 10 igual a numerador começar estilo mostrar 9 sobre 2 fim do estilo sobre denominador z fim da fração z igual a numerador começar estilo mostrar 90 sobre 2 fim do estilo sobre denominador 6 fim da fração z igual a 45 sobre 6 seta dupla para a direita z igual a 15 sobre 2

Somando os valores encontrados, temos:

y mais m mais z igual a 15 mais 9 sobre 2 mais 15 sobre 2 y mais m mais z igual a numerador 30 mais 9 mais 15 sobre denominador 2 fim da fração y mais m mais z igual a 54 sobre 2 y mais m mais z igual a 27

27 é um número divisível por 3, pois 3.9 = 27.

Alternativa: a) 3

Questão 8

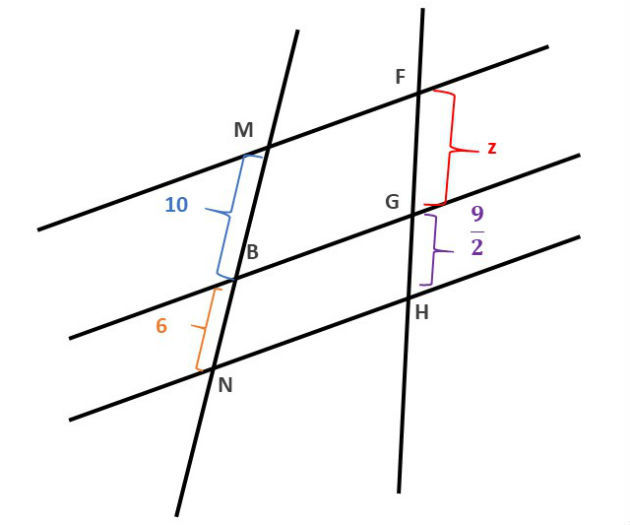
(Cefet/MG - 2014) Considere a figura em que r itálico paralelo s itálico paralelo t

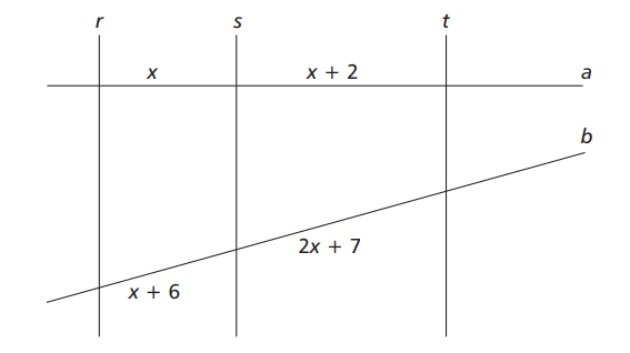
Questão Cefet-MG 2014 Teorema de Tales

O valor de x é

a) 3.
b) 4.
c) 5.
d) 6.

Alternativa correta: b) 4

Para encontrar o valor do x, iremos aplicar o teorema de Tales. O cálculo será feito utilizando a seguinte proporção:

numerador x sobre denominador x mais 6 fim da fração igual a numerador x mais 2 sobre denominador 2 x mais 7 fim da fração parêntese esquerdo 2 x mais 7 parêntese direito. x igual a parêntese esquerdo x mais 2 parêntese direito. parêntese esquerdo x mais 6 parêntese direito 2 x ao quadrado mais 7 x igual a x ao quadrado mais 6 x mais 2 x mais 12 2 x ao quadrado menos x ao quadrado mais 7 x menos 8 x menos 12 igual a 0 x ao quadrado menos x menos 12 igual a 0 incremento igual a 1 menos 4. parêntese esquerdo menos 12 parêntese direito.1 incremento igual a 1 mais 48 incremento igual a 49 x com 1 subscrito igual a numerador 1 mais 7 sobre denominador 2 fim da fração igual a 4 x com 2 subscrito igual a numerador 1 menos 7 sobre denominador 2 fim da fração igual a menos 3 espaço espaço espaço espaço parêntese esquerdo d e s p r e z a m o s espaço e s t e espaço v a l o r vírgula espaço p o r espaço s e r espaço u m a espaço m e d i d a espaço d e espaço s e g m e n t o parêntese direito

Alternativa: b) 4

Questão 9

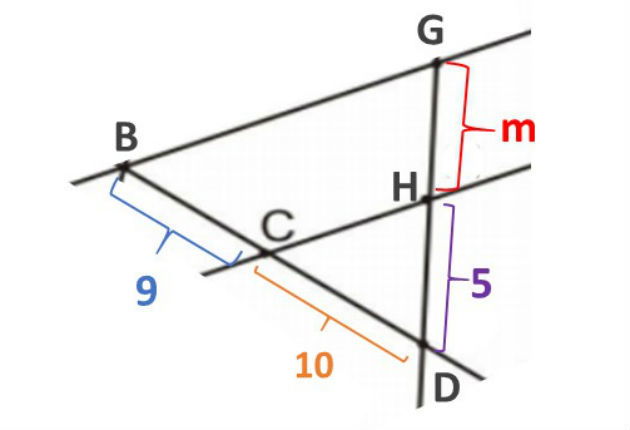
(Colégio Pedro II - 2012) Para melhorar a qualidade do solo, aumentando a produtividade do milho e da soja, em uma fazenda é feito o rodízio entre essas culturas e a área destinada ao pasto. Com essa finalidade, a área produtiva da fazenda foi dividida em três partes conforme a figura.

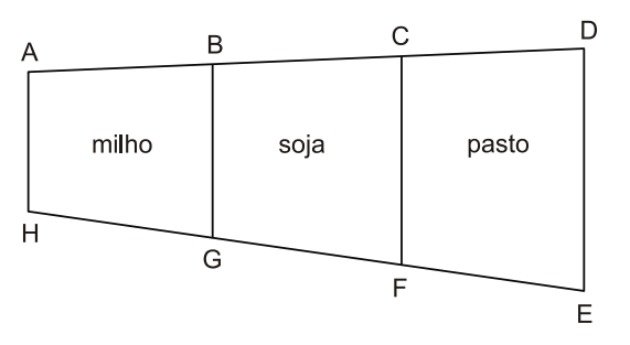
Questão Colégio Pedro II Teorema de Tales

Considere que

  • os pontos A, B, C e D estão alinhados;
  • os pontos H, G, F e E estão alinhados;
  • os segmentos A H em moldura superior fecha moldura vírgula espaço B G em moldura superior fecha moldura vírgula espaço C F em moldura superior fecha moldura espaço e espaço D E em moldura superior fecha moldurasão, dois a dois, paralelos entre si;
  • AB = 500 m, BC = 600 m, CD = 700 m e HE = 1980 m.

Nessas condições, a medida do segmento G F em moldura superior fecha moldura é, em metros,

a) 665.
b) 660.
c) 655.
d) 650.
e) 645.

Alternativa correta: b) 660

Os segmentos indicados são dois a dois paralelos entre si, então, pelo teorema de Tales, sabemos que formam um proporção.

Como o valor informado foi do segmento H E em moldura superior fecha moldura, que é a soma dos segmentos H G em moldura superior fecha moldura vírgula espaço G F em moldura superior fecha moldura espaço e espaço F E em moldura superior fecha moldura, utilizaremos também a soma dos segmentos A B em moldura superior fecha moldura vírgula espaço B C em moldura superior fecha moldura espaço e espaço C D (500 + 600 + 700 = 1800 m).

Assim, temos a seguinte proporção:

1800 sobre 1980 igual a numerador 600 sobre denominador G F fim da fração G F igual a numerador 1980.600 sobre denominador 1800 fim da fração G F igual a 660 espaço m

Alternativa: b) 660

Questão 10

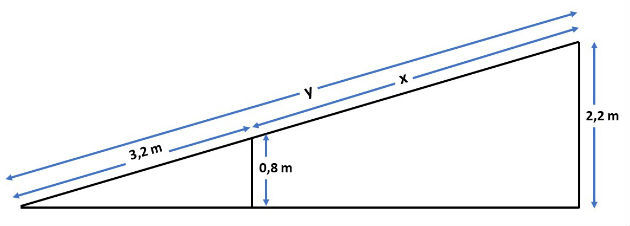
(Enem - 2009) A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2 metros. Um paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8 metros. A distância em metros que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é

a) 1,16 metros.
b) 3,0 metros.
c) 5,4 metros.
d) 5,6 metros.
e) 7,04 metros.

Alternativa correta: d) 5,6 metros

Podemos representar a situação proposta no problema conforme a figura abaixo:

Questão Enem 2009 teorema de tales

Note que as duas alturas indicadas formam um ângulo de 90º com o solo, desta forma, essas duas retas são paralelas.

Considerando o solo e a rampa duas retas transversais a essas retas paralelas, podemos aplicar o teorema de Tales.

Para isso, usaremos a seguinte proporção:

numerador 3 vírgula 2 sobre denominador 0 vírgula 8 fim da fração igual a numerador y sobre denominador 2 vírgula 2 fim da fração 0 vírgula 8 y igual a 3 vírgula 2.2 vírgula 2 0 vírgula 8 y igual a 7 vírgula 04 y igual a numerador 7 vírgula 08 sobre denominador 0 vírgula 8 fim da fração y igual a 8 vírgula 8 espaço m

Como queremos descobrir quanto ainda falta para a pessoa caminhar, devemos fazer:

x = 8,8 - 3,2
x = 5,6 m

Alternativa: d) 5,6 metros

Questão 11

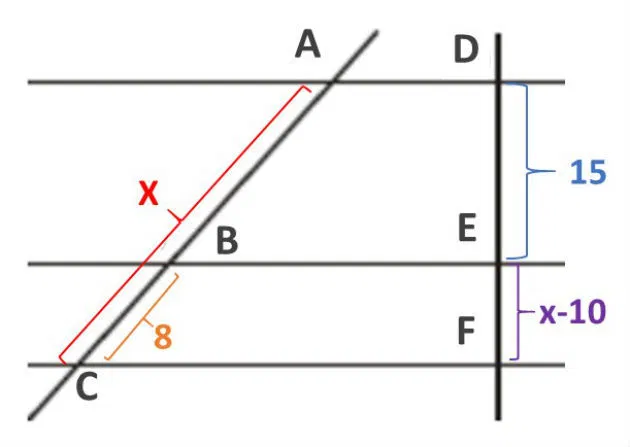
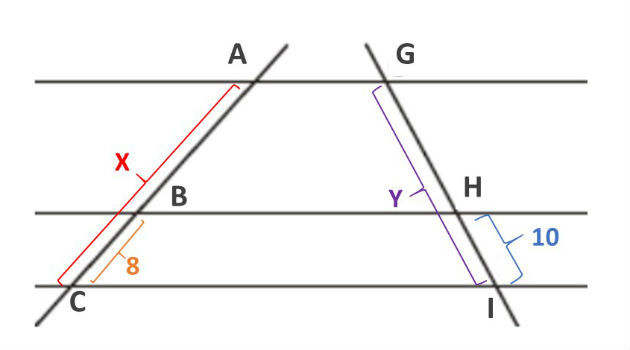
(PUC/Campinas - 2007) Na figura a seguir, as retas r, s e t são paralelas entre si

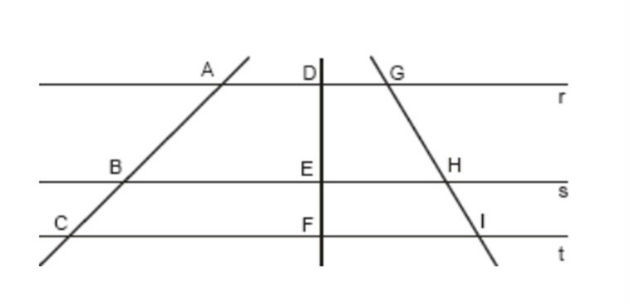
Questão puc-campinas 2007 teorema de tales

Se AC = x, BC = 8, DE = 15, EF = x - 10, GI = y e HI = 10, então x + y é um número

a) maior que 47
b) entre 41 e 46
c) menor que 43
d) quadrado perfeito
e) cubo perfeito

Alternativa correta: b) entre 41 e 46

Primeiro, vamos encontrar o valor do x usando os seguintes segmentos:

Questão puc-campinas 2007 teorema de tales

Pela figura, identificamos que o segmento AB é igual a x - 8, desta forma, aplicando o teorema de Tales, temos a seguinte proporção:

numerador parêntese esquerdo x menos 8 parêntese direito sobre denominador 8 fim da fração igual a numerador 15 sobre denominador parêntese esquerdo x menos 10 parêntese direito fim da fração parêntese esquerdo x menos 8 parêntese direito. parêntese esquerdo x menos 10 parêntese direito igual a 15.8 x ao quadrado menos 10 x menos 8 x mais 80 igual a 120 x ao quadrado menos 18 x menos 40 igual a 0 incremento igual a 324 mais 160 incremento igual a 484 x com 1 subscrito igual a numerador 18 mais 22 sobre denominador 2 fim da fração igual a 40 sobre 2 igual a 20 x com 2 subscrito igual a numerador 18 menos 22 sobre denominador 2 fim da fração igual a numerador menos 4 sobre denominador 2 fim da fração igual a menos 2

Como o valor do x representa a medida de um segmento, vamos desconsiderar o valor negativo.

Podemos agora calcular o valor do y. Substituindo o valor encontrado para x, temos a seguinte figura:

Questão puc-campinas 2007 teorema de tales

20 sobre 8 igual a y sobre 10 200 sobre 8 igual a y y igual a 25

Assim, a soma de x e y será igual a:

x + y = 20 + 25 = 45

Portanto, a resposta é um número entre 43 e 46.

Alternativa: b) entre 41 e 46

Questão 12

(Cefet/PR - 2006) O jardineiro Sr. Artur fez um canteiro triangular composto por folhagens e flores onde as divisões são todas paralelas à base.

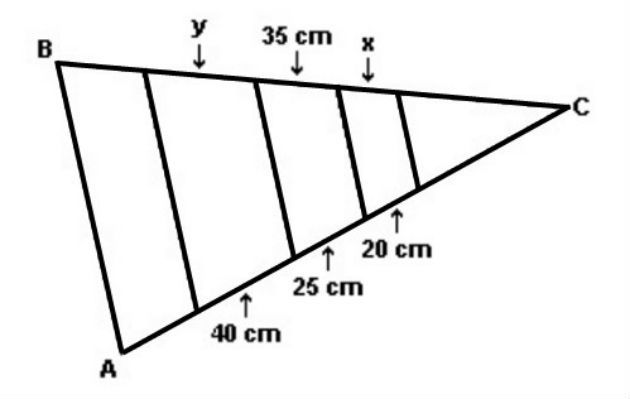
Questão cefet-PR 2006 Teorema de Tales

Sendo assim, as medidas x e y dos canteiros de flores são, respectivamente:

a) 30 cm e 50 cm.
b) 28 cm e 56 cm.
c) 50 cm e 30 cm.
d) 56 cm e 28 cm.
e) 40 cm e 20 cm.

Alternativa correta: b) 28 cm e 56 cm.

Sendo todas as divisões paralelas, os segmentos formados são proporcionais, então, usaremos as seguintes proporções:

x sobre 20 igual a 35 sobre 25 x igual a numerador 35.20 sobre denominador 25 fim da fração x igual a 28 espaço c m y sobre 40 igual a 35 sobre 25 y igual a numerador 35.40 sobre denominador 25 fim da fração y igual a 56 espaço c m

Alternativa: b) 28 cm e 56 cm.

Estude também sobre Teorema de Pitágoras.

Continue praticando com:

Rafael C. Asth
Rafael C. Asth
Professor de Matemática licenciado, pós-graduado em Ensino da Matemática e da Física e Estatística. Atua como professor desde 2006 e cria conteúdos educacionais online desde 2021.
Veja também